Notes
three squares vii solution
Solution to the Three Squares VII Puzzle
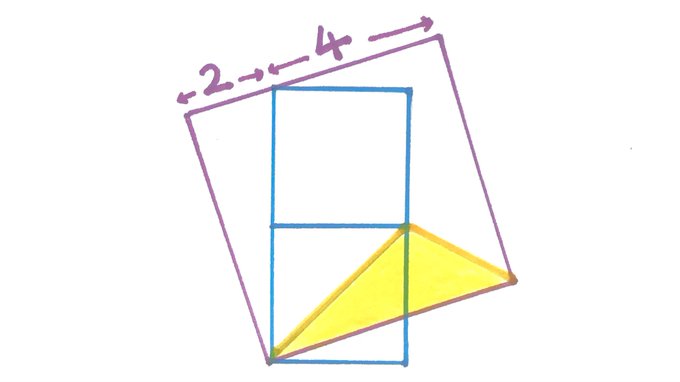
Three squares. What’s the shaded area?
Solution by Pythagoras' Theorem, Similar Triangles, and the Area of a Triangle
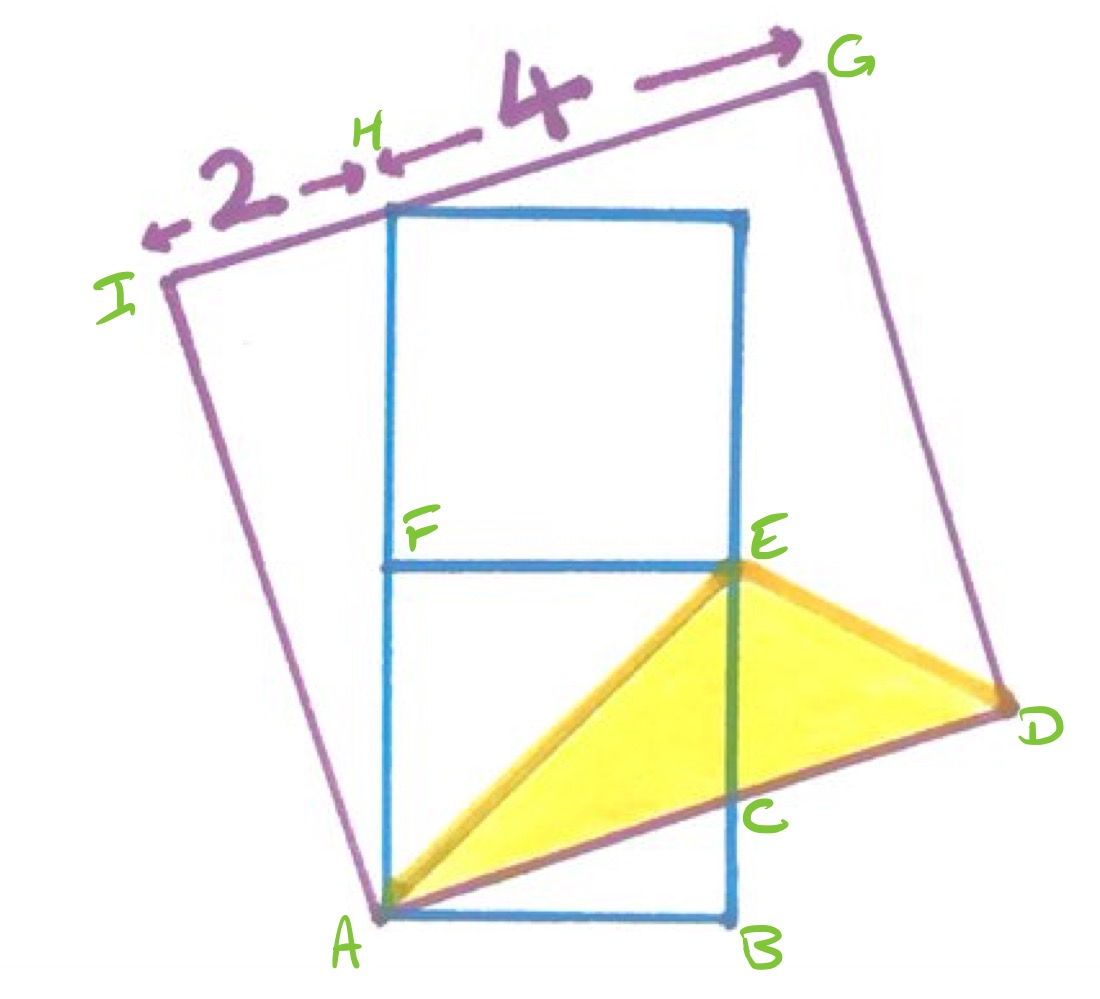
Label the points as above.
The side length of the outer square is , and triangle is right-angled so Pythagoras' Theorem applies. This means that has length given by:
So line segment has length and the area of the smaller squares is . Triangle therefore has area .
Angle is equal to angle since both are . Therefore, triangles and are similar. This means that the lengths of line segments and are in the ratio , so then as and have the same length, divides in the ratio . This means that triangle has area two thirds of , so has area .
The scale factor from triangle to is , so line segment has length:
By the area of a triangle, taking as the base of triangle , point therefore has height above , and therefore above . So then triangle has area .