Notes
three squares vi solution
Solution to the Three Squares VI Puzzle
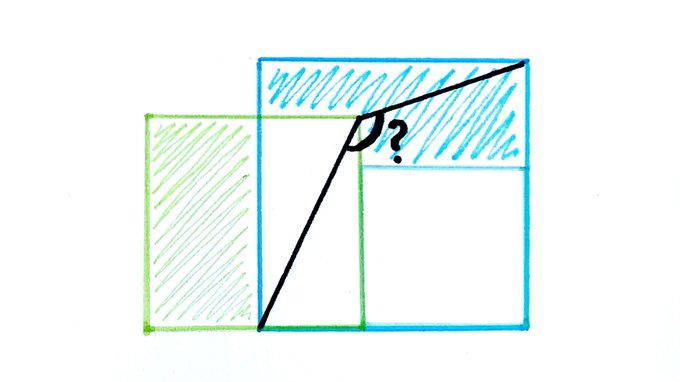
The blue and green shaded regions created by these three squares have the same area. What’s the angle?
Solution by Pythagoras' Theorem and Angles in a Quadrilateral
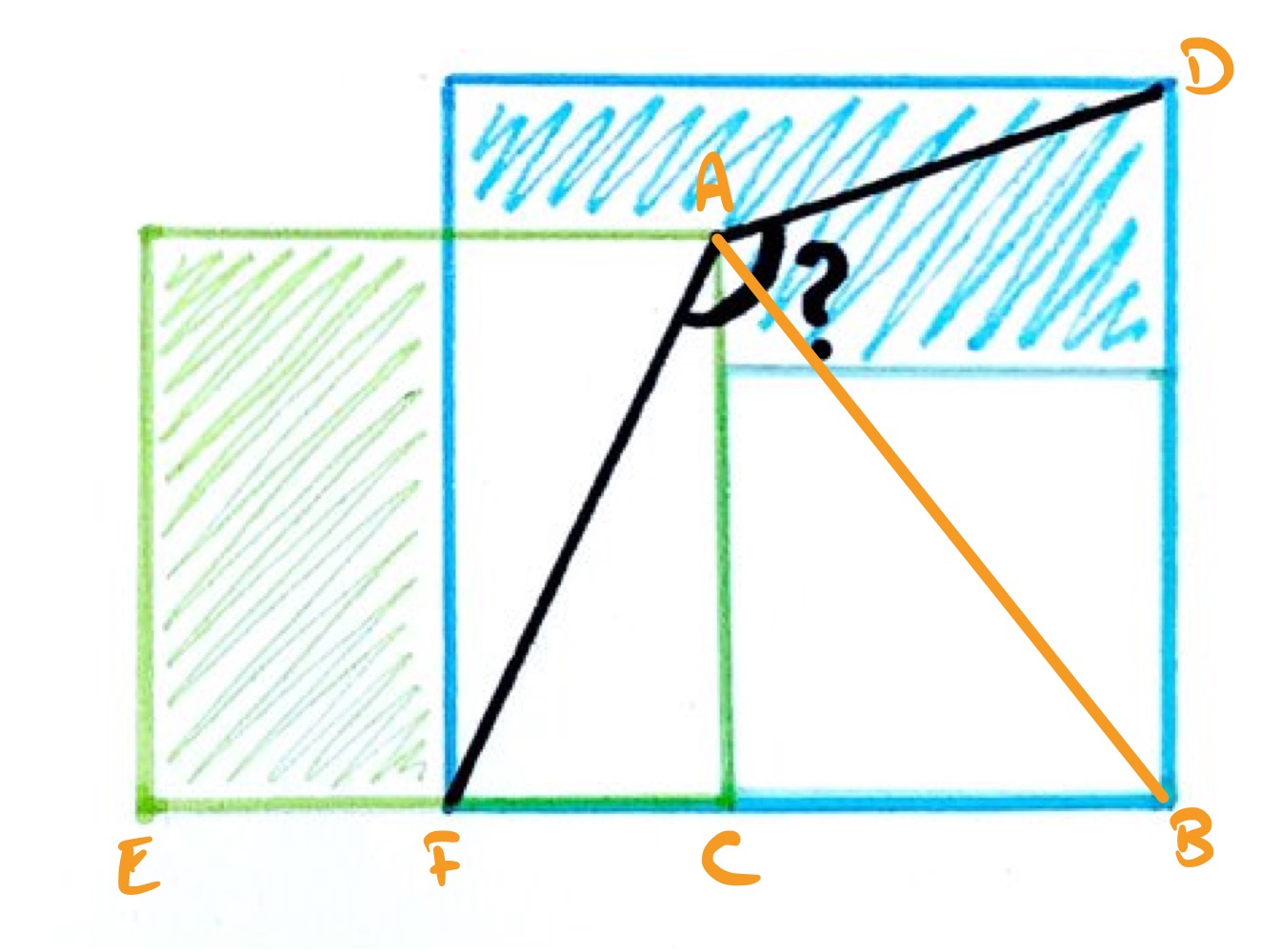
Let the side lengths of the squares be , , and in increasing order.
Then has length so the green region has area .
The line segment has length , so the blue region has area:
These areas are the same, so:
This means that the lengths , , and form the sides of a right-angled triangle, by the converse to Pythagoras' theorem. Triangle is a right-angled triangle with sides and , so its hypotenuse, , has length .
This means that triangles and are both isosceles with angles and equal to each other, and and also equal to each other.
Then as the angles in a quadrilateral add up to :
Hence the angle is .