Notes
three squares v solution
Solution to the Three Squares V Puzzle
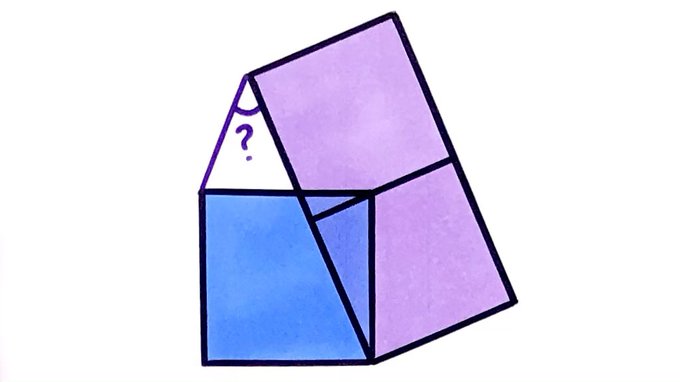
Three squares. What’s the angle?
Solution by Angle at the Circumference is Half the Angle at the Centre
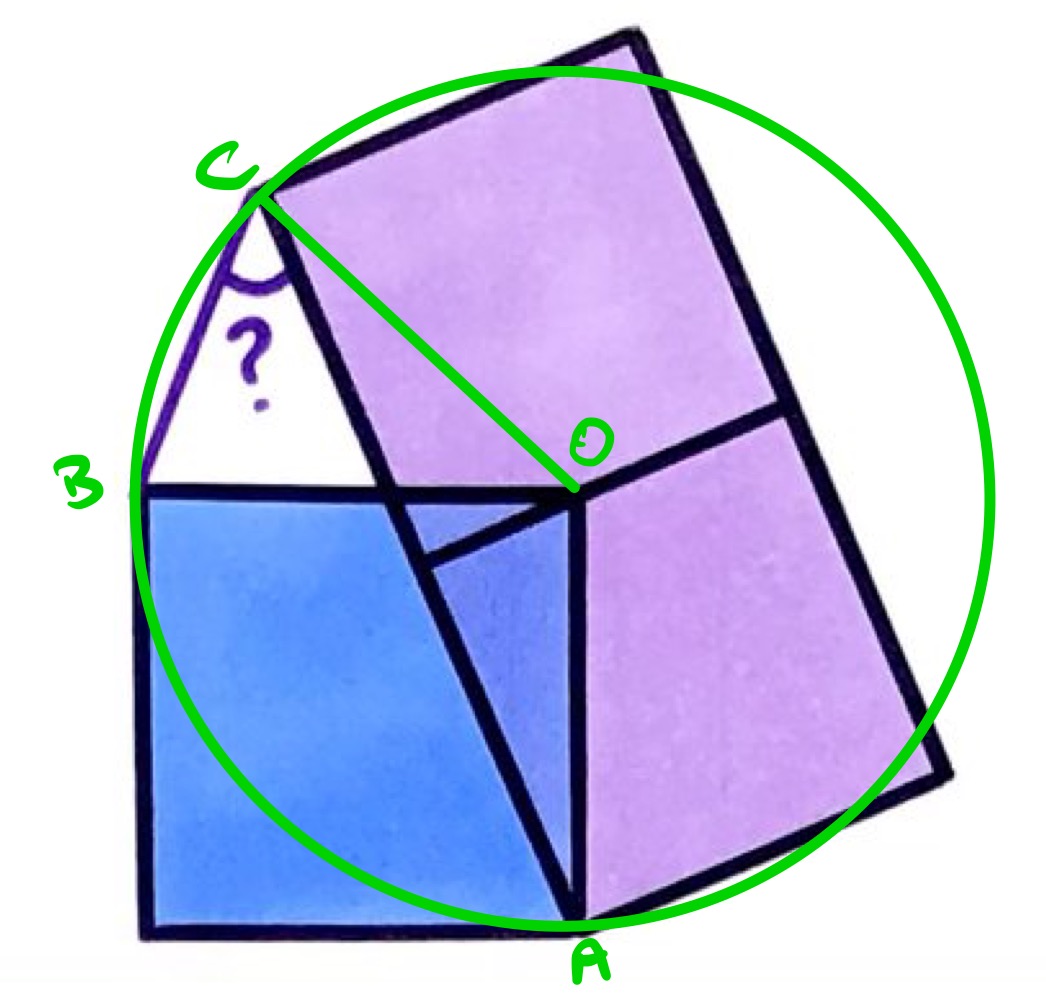
With the points labelled as above, the length of is the same as , hence also the same as . Therefore a circle with centre that passes through also passes through and . Then since the angle at the circumference is half the angle at the centre, angle is half of angle , which is as it is the corner of a square. Hence angle is .
Solution by Invariance Principle
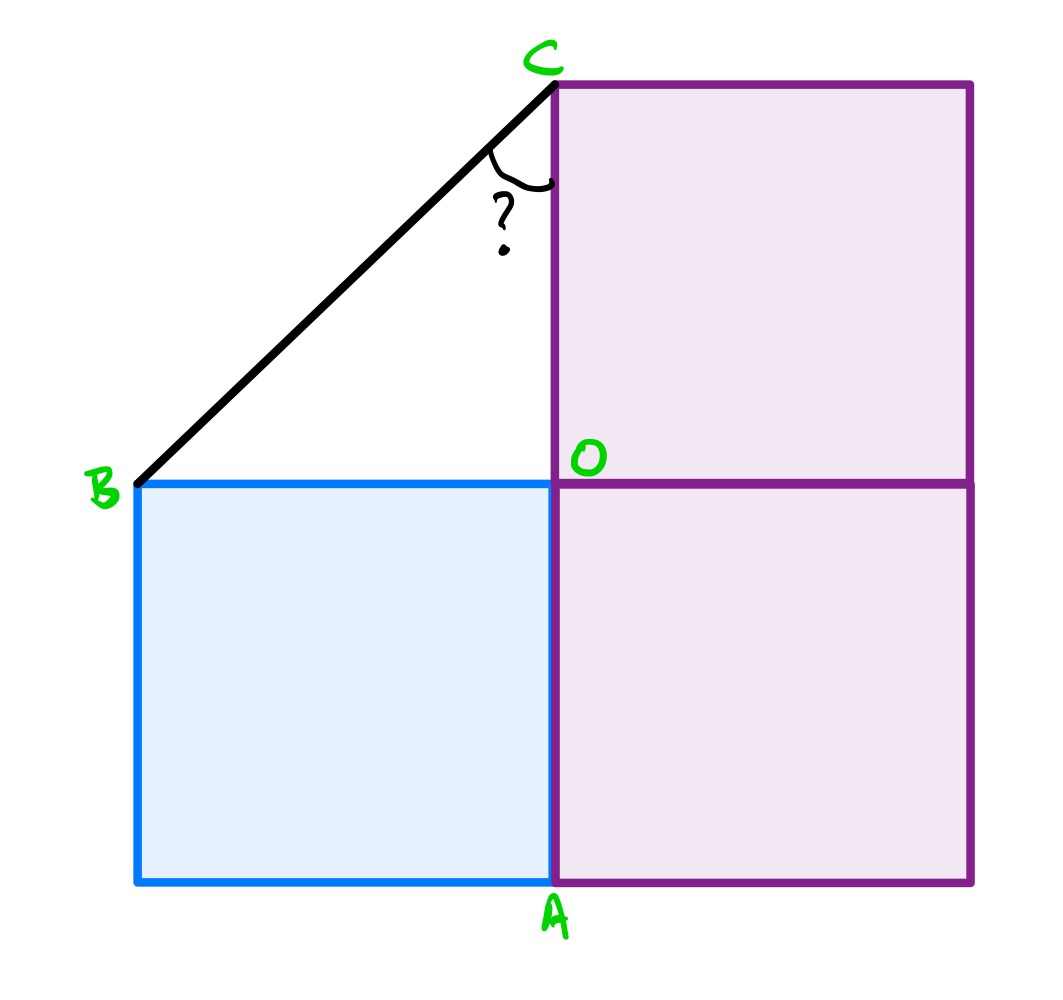
The purple squares can be tilted, providing remains on the joining line. With the configuration above, the purple squares are the same size as the blue square, and so the triangle is an isosceles right-angled triangle so angle is .