Notes
three squares solution
Solution to the Three Squares Puzzle
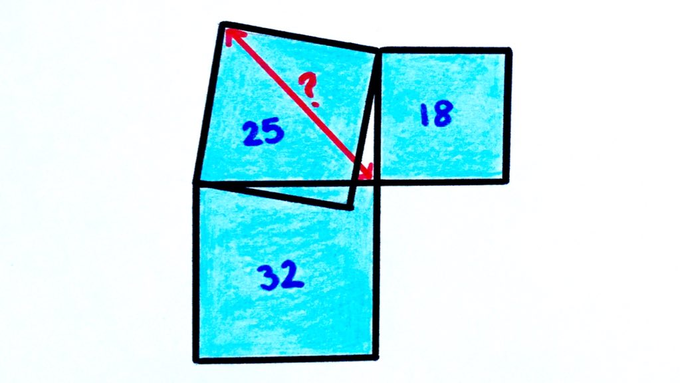
The areas of the three squares are given. How long is the red line?
Solution by Properties of Right-Angled Triangles and Congruent Triangles
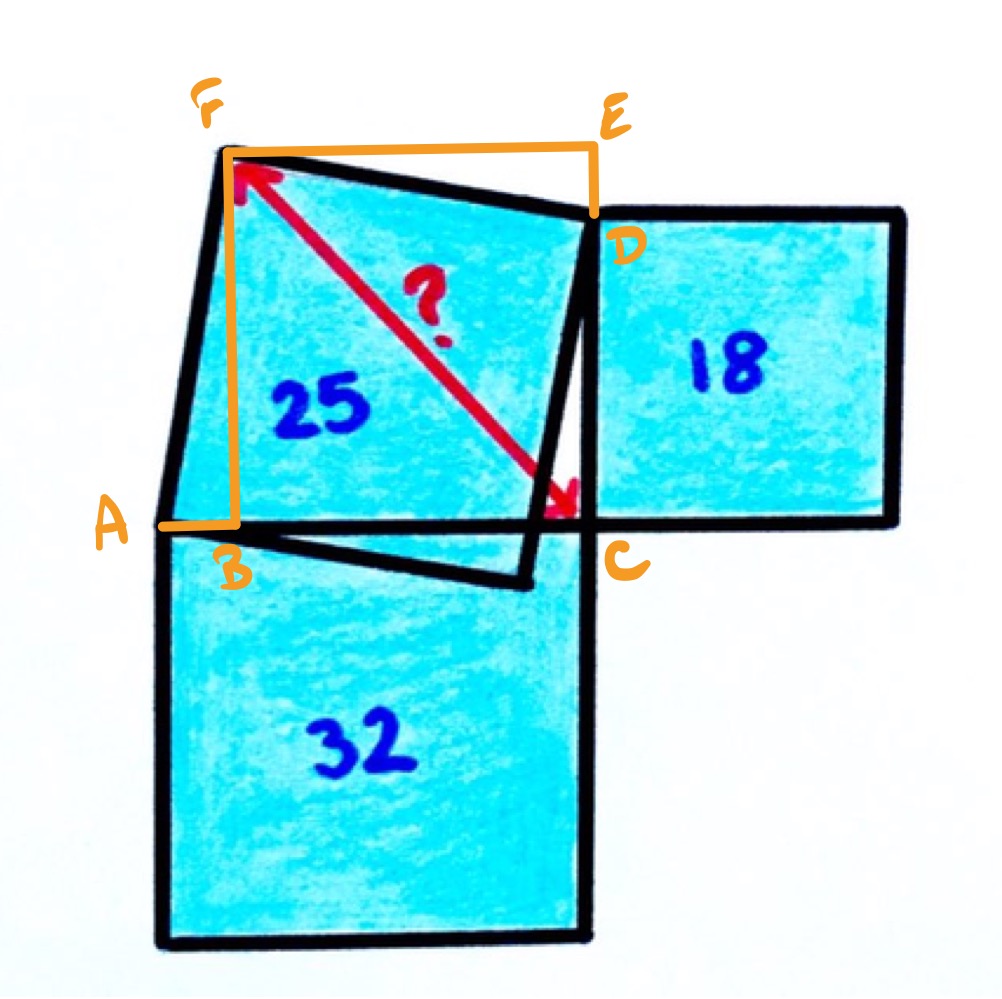
With the points labelled as above, the side lengths of the squares are , , and $5.
Point is such that triangle is right-angled, and so also point is such that is also right-angled. Angles and are equal, as both add to angle to make a right-angle. Therefore, triangles and are congruent.
Let line segment have length and have length . Then these are also the lengths of line segments and , respectively. Translating line segment along shows that the lengths of and add up to , similarly the difference of the length of and of is . That is, and . Hence .
Triangle is right-angled and isosceles with shorter side length . Its diagonal is therefore .
Hence line segment has length .