Notes
three squares overlapping a semi-circle solution
Solution to the Three Squares Overlapping a Semi-Circle Puzzle
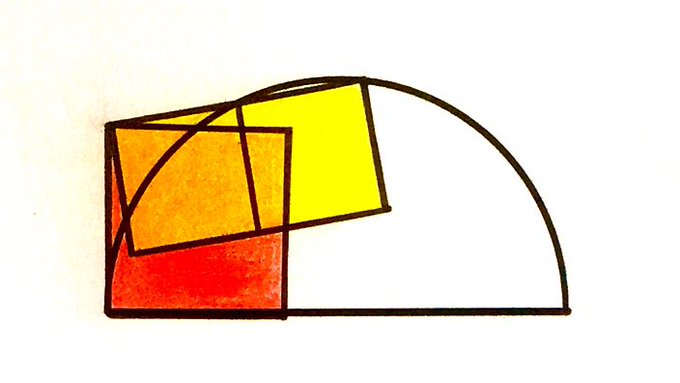
The two smaller squares each have area . What’s the area of the larger square?
Solution by Intersecting Chords Theorem
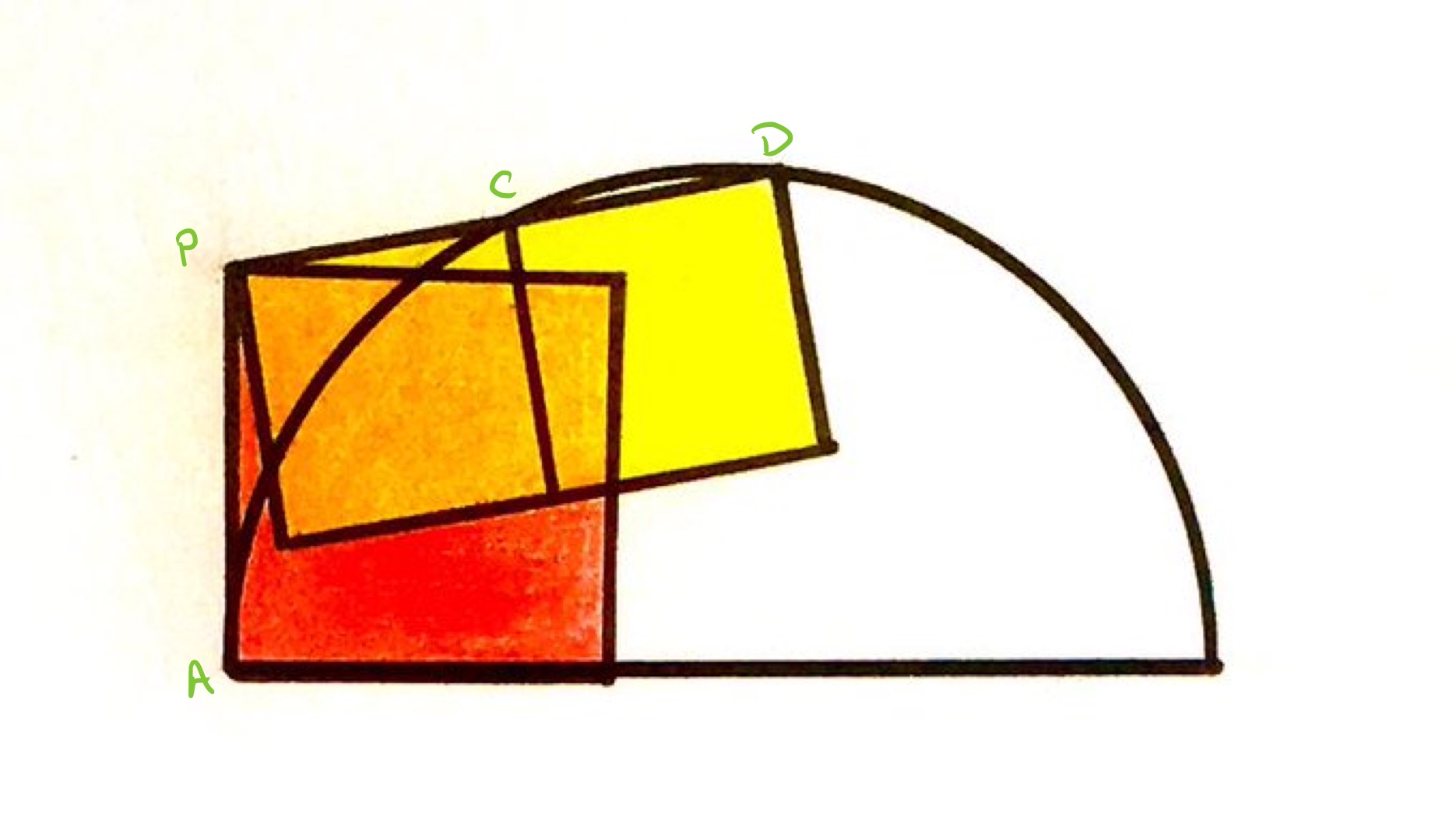
As is at right-angles to the diameter of the semi-circle, it is a tangent to it at . The intersecting chords theorem then says that:
Each small square has area so has side length . Therefore has length and length . Hence the area of the red square is .