Notes
three squares inside a triangle solution
Solution to the Three Squares Inside a Triangle Puzzle
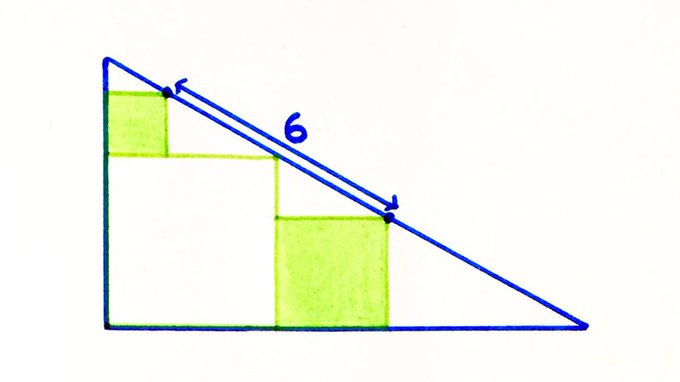
Three squares inside a triangle. What’s the sum of the two shaded areas?
Solution by Similar Triangles and Pythagoras' Theorem
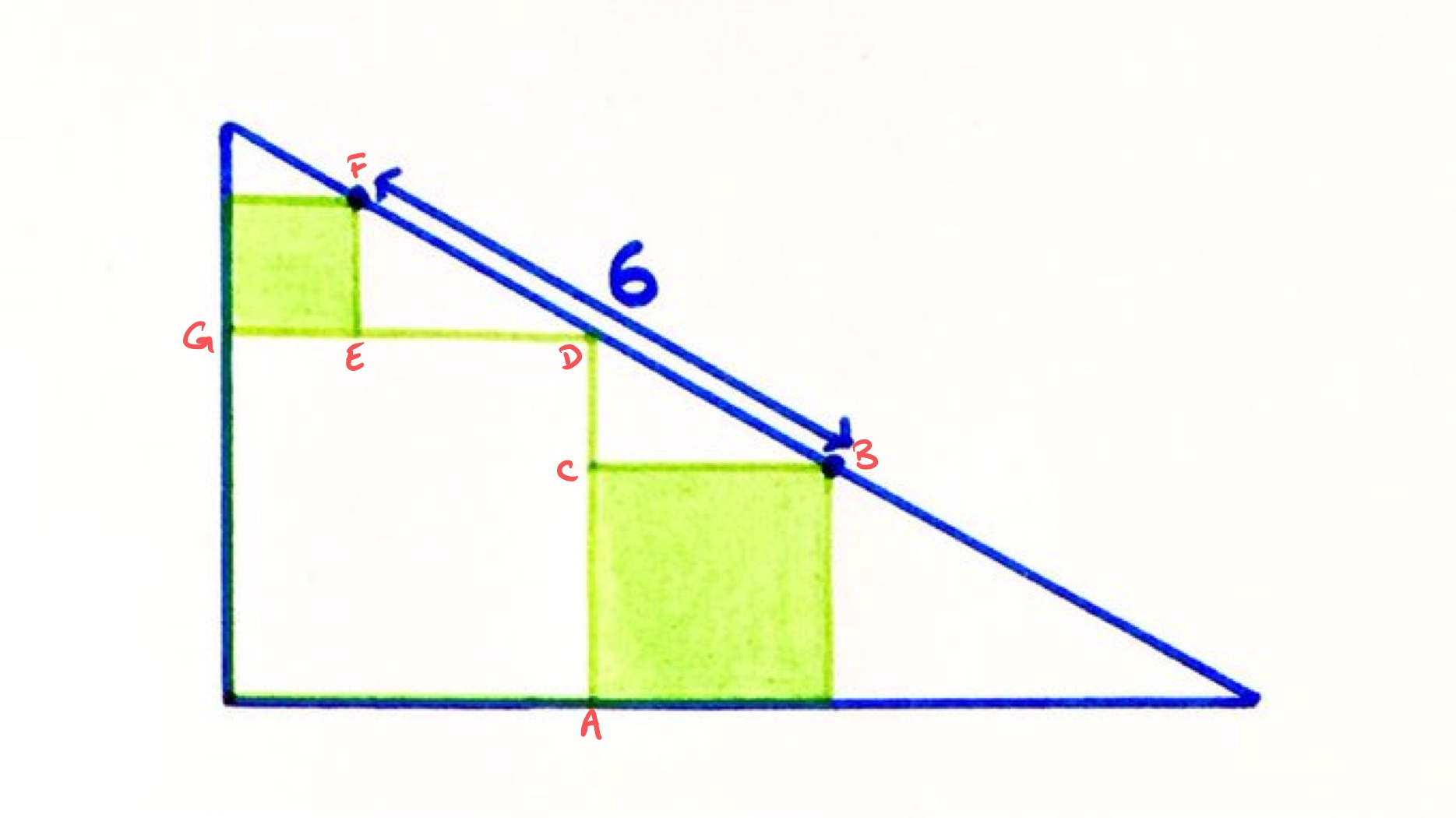
With the points labelled as in the above diagram, triangles and are similar. The lengths of and are the same, and the lengths of and are the same. So the full length of is the sum of the lengths of and , and the full length of is the same as the sum of the lengths of and . These are sides of the white square, so and are the same length, and so the triangles and are actually congruent.
This means that the length of is half of that of , so is . Also and are the same length. Writing for the length of and for the length of , the sum of the two shaded areas is . Applying Pythagoras' theorem to triangle shows that so the sum of the two shaded areas is .