Notes
three squares in a triangle solution
Three Squares in a Triangle
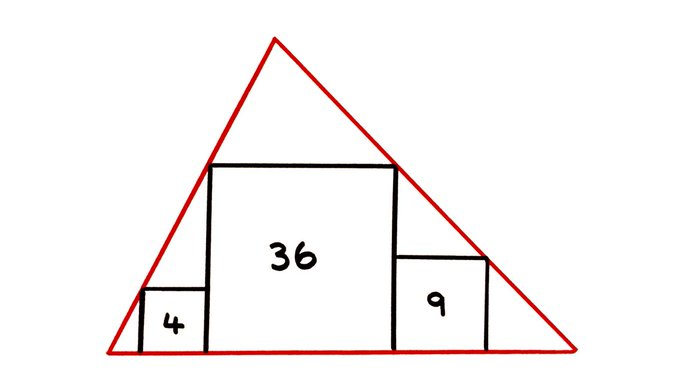
The areas of the three squares are given. What’s the area of the red triangle?
Solution by Similar Triangles
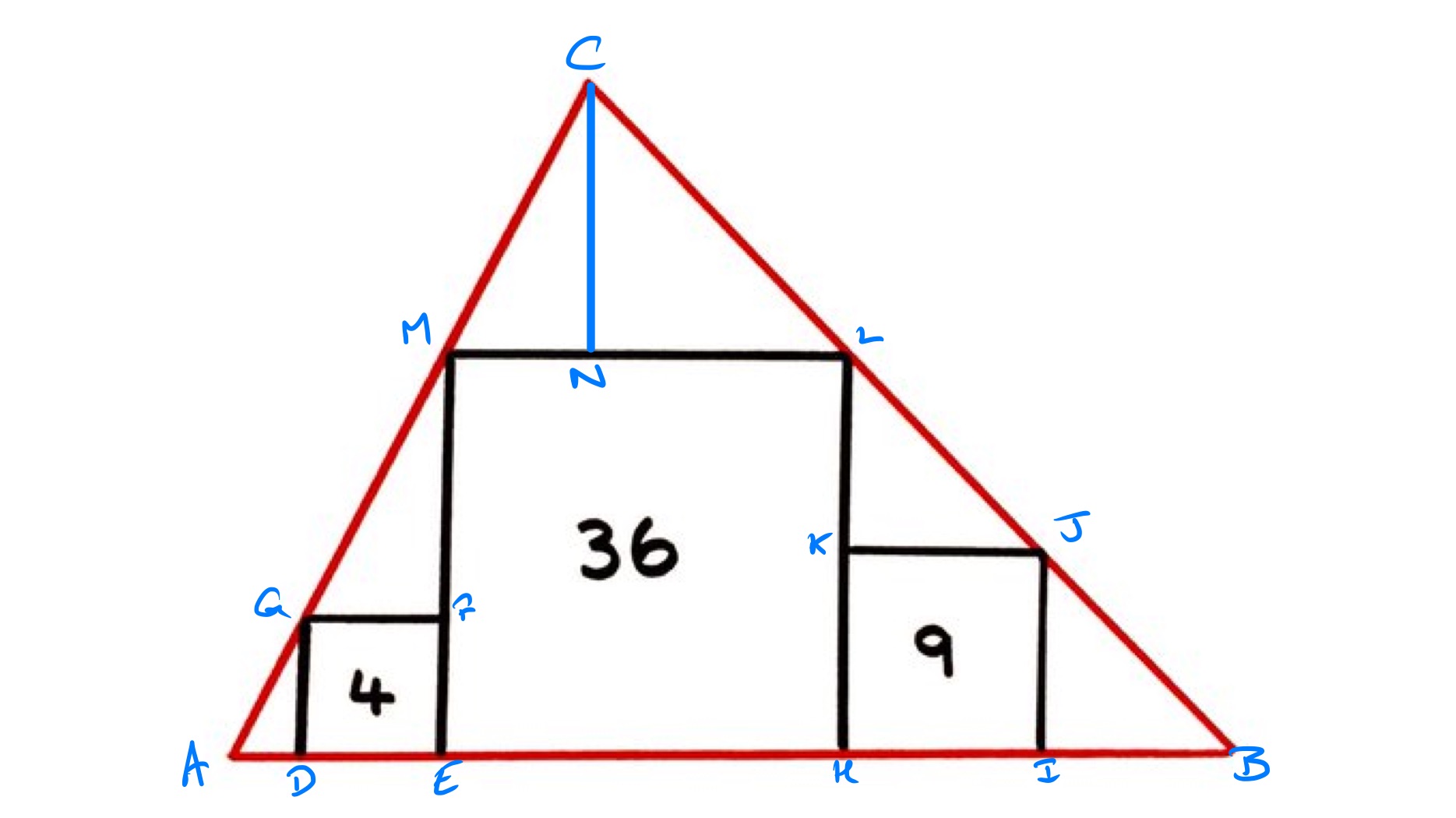
With the points labelled as above, the areas of the squares mean that the side lengths are as follows: the length of is , the length of is , and the length of is .
Then has length which is the same length as so triangle is an isosceles right-angled triangle. Triangles and are similar to this triangle, so also has length and is the same length as .
On the other side, has length so in right-angled triangle , the lengths of the horizontal to vertical sides are in the ratio . This means that has length and the length of is half that of .
Putting these together, the length of is times the length of , so the length of is as that of is .
The length of the base of the triangle, so of , is then and its height is . Therefore its area is .