Notes
three squares in a semi-circle solution
Solution to the Three Squares in a Semi-Circle Puzzle
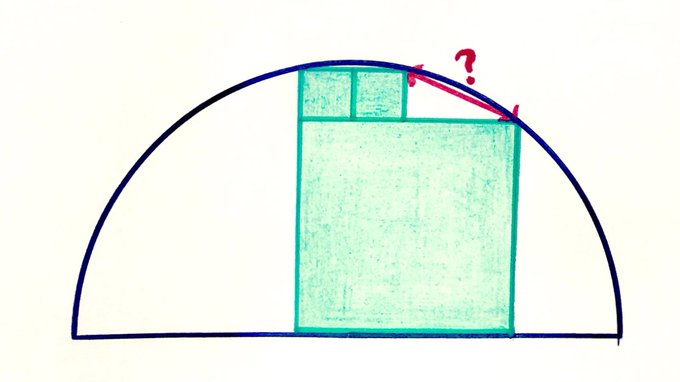
The two smallest squares each have area . How long is the red line?
Solution by Pythagoras' Theorem
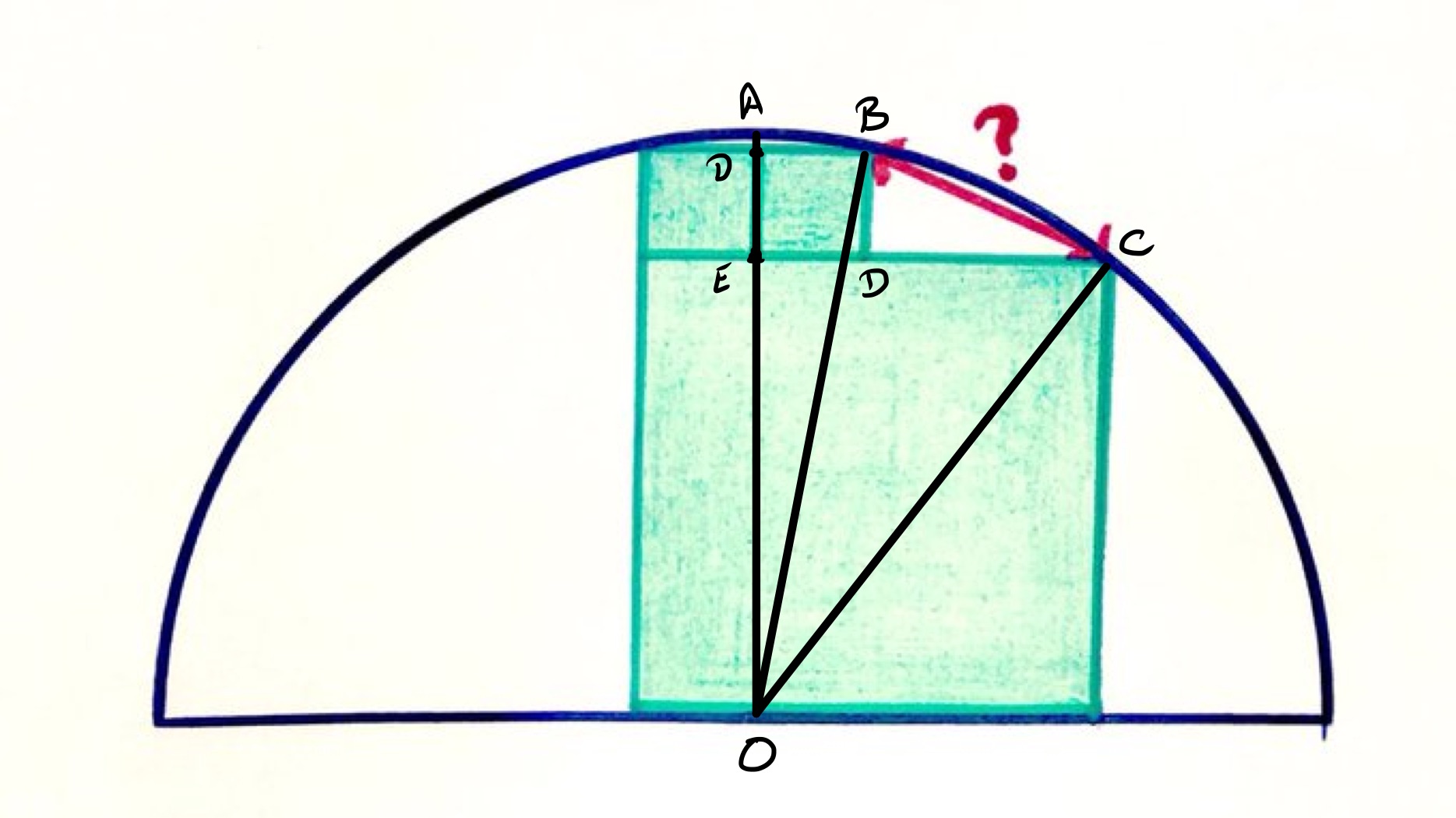
Let be the side length of the smallest squares, so that , and let be the side length of the larger one. As the perpendicular bisector of a chord passes through the centre of the circle, the continuation of passes through the centre of the circle at .
Triangle is right-angled with of length and of length . The desired length, , is the hypotenuse of this triangle so by Pythagoras' theorem the square of its length is given by:
Let be the radius of the circle. Triangle is right-angled with side lengths , , and , so by Pythagoras' theorem:
Triangle is also right-angled and its side lengths are , , and so:
Subtracting the second equation from the first gives:
Adding this to the equation for the square of the length of gives that that quantity is which is . Therefore, the length of is .