Notes
three squares in a circle ii solution
Solution to the Three Squares in a Circle II Puzzle
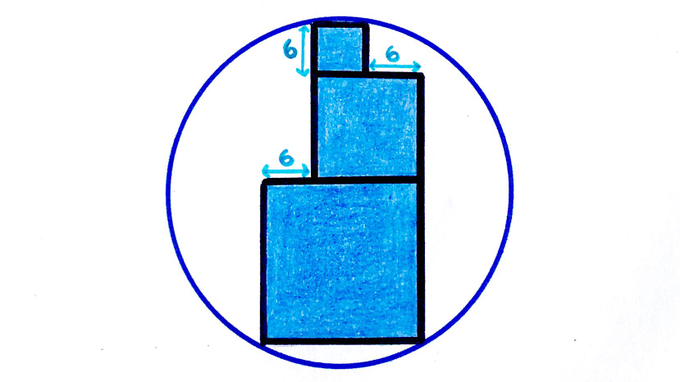
Three squares inside a circle. What’s the circle’s area?
Solution by Pythagoras' Theorem, Difference of Two Squares, and Area of a Circle
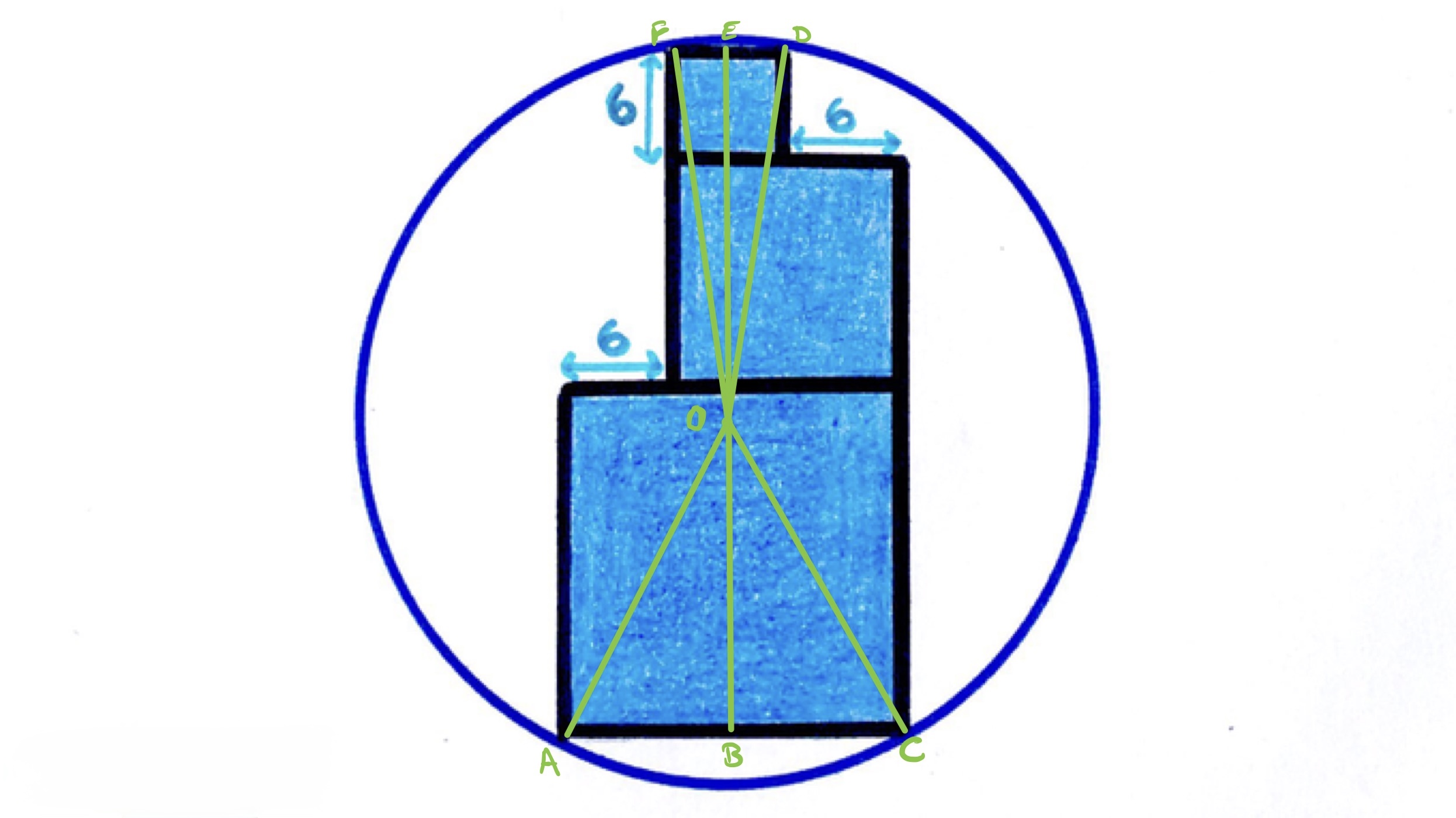
In the diagram above, is the centre of the circle and is perpendicular to the sides of the squares at and . The squares have side lengths , , and . Therefore, has length .
Let be the radius of the circle. Let be the length of and the length of , so . Applying Pythagoras' theorem to triangle shows that:
and applying it to triangle shows that:
Subtracting these equations shows that:
Since , and by difference of two squares this means that . So and .
Then .
The area of the circle is therefore .