Notes
three squares iii solution

Solution to the Three Squares III Puzzle

Solution by Angle at the Circumference is Half the Angle at the Centre

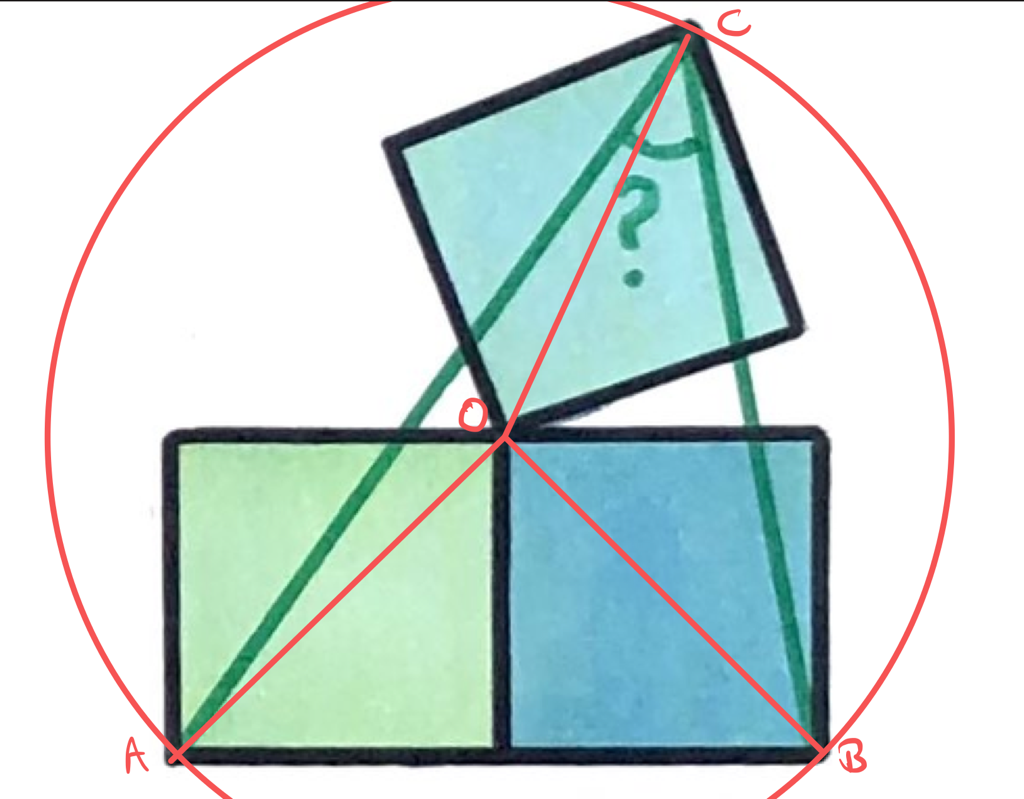
With the points labelled as above, the line segments $O A$, $O B$, and $O C$ are all diagonals of congruent squares, so are the same length. Therefore the circle centre $O$ that passes through $A$ also passes through $B$ and $C$.

Then since the angle at the circumference is half the angle at the centre, angle $A \hat{C} B$ is half angle $A \hat{O} B$. But this is $90^\circ$ as it is formed from the diagonals of two adjacent squares.

Hence angle $A \hat{C} B = 45^\circ$.

Solution by Isosceles Triangles and Angles in a Triangle

With the same labelling as above, triangles $O A C$, $O B A$, and $O C B$ are isosceles. Since $O A$ and $O B$ are the diagonals of squares, angles $O \hat{A} B$ and $O \hat{B} A$ are both $45^\circ$. Since the angles in triangle $A B C$ add up to $180^\circ$, this means that the sum of angles $O \hat{A} B$, $O \hat{C} A$, $O \hat{C} B$, and $O \hat{B} C$ is $90^\circ$.

Then since triangles $O A C$ and $O B C$ are isosceles, angles $O \hat{A} C$ and $O \hat{C} A$ are equal to each other, as are angles $O \hat{B} C$ and $O \hat{C} B$. Therefore, angle $A \hat{C} B$ is half of $90^\circ$ so is $45^\circ$.

Solution by Agg Invariance Principle and Angles in a Square

The upper square is tilted, but the angle of the tilt is not specified. A special case is where it aligns with the right-hand lower square, as in the diagram below.

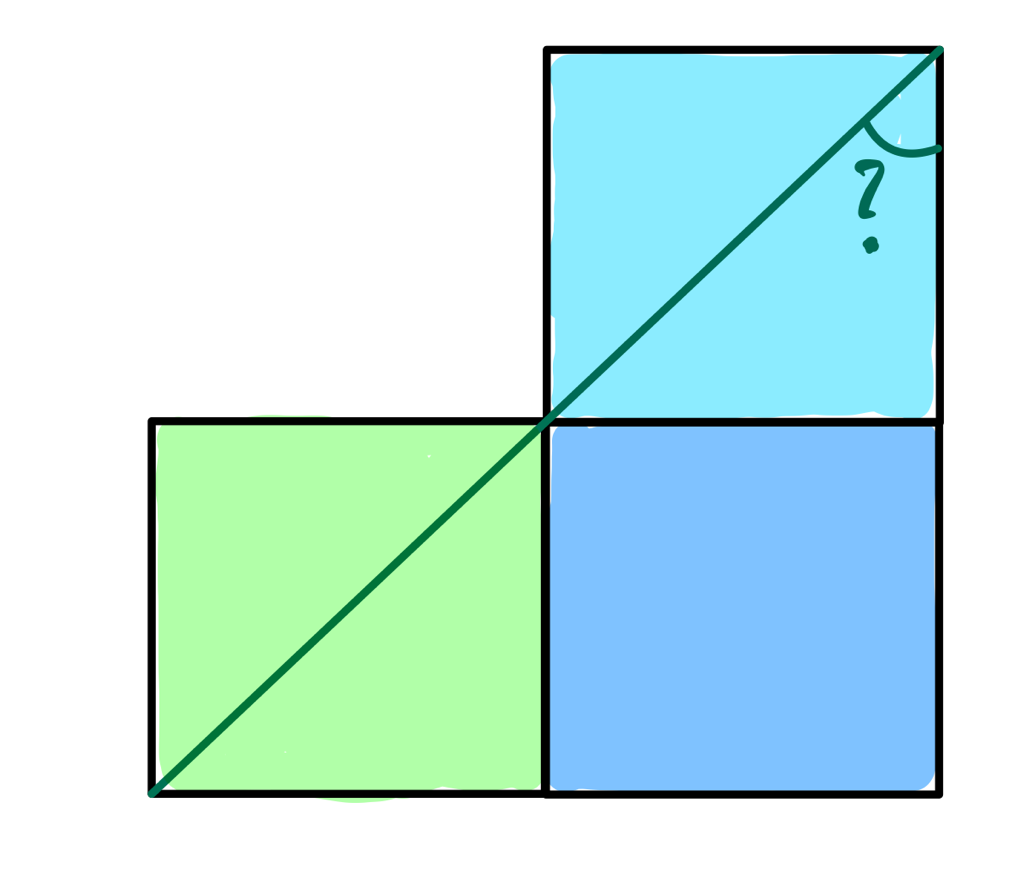
In this case, the requested angle is the angle between a diagonal and side in a square, hence is $45^\circ$.