Notes
three squares ii solution
Solution to the Three Squares (II) Puzzle
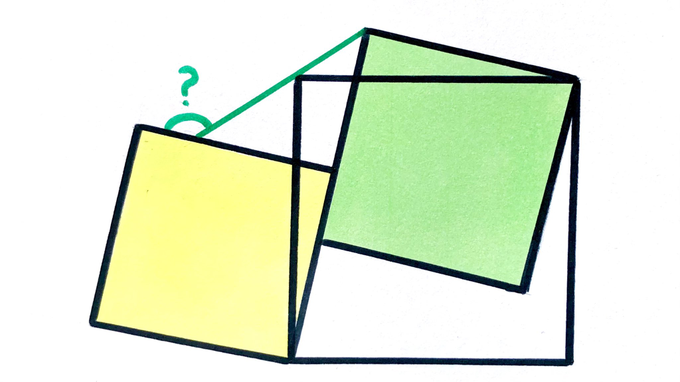
Three squares. What’s the angle?
Solution by Calculating Angles
The key to this solution is to spot the right-angled triangles. Let us label the vertices as in the following diagram.
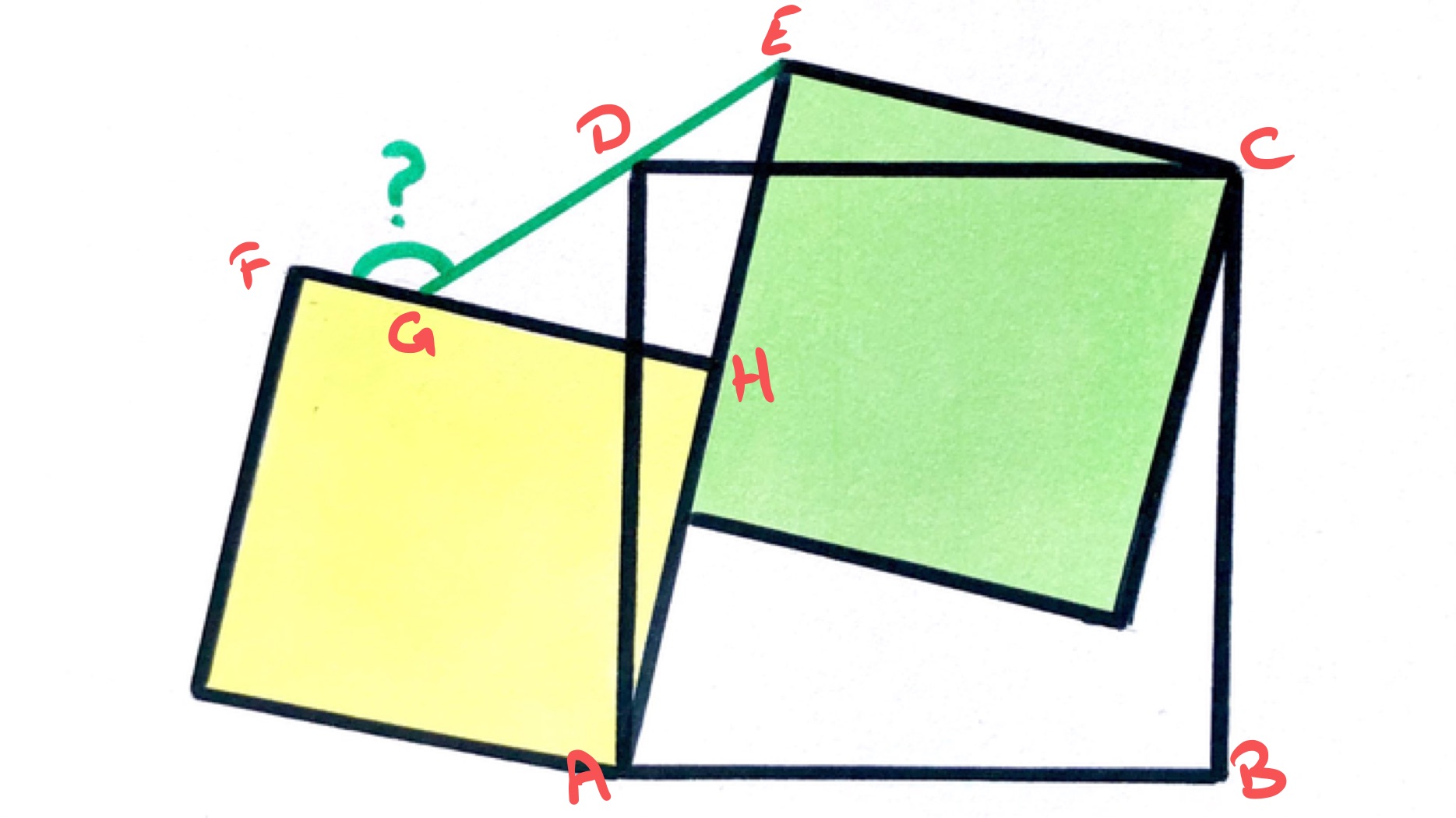
Then triangle is a right-angled triangle, as is triangle . In both of these then is the hypotenuse. Marking the midpoint of the hypotenuse and joining it to the vertex with the right-angle splits a right-angled triangle into two isosceles triangles (see right-angled triangle for details).
The quadrilateral therefore splits into three isosceles triangles, as in the following diagram.
Now, the interior angles of a quadrilateral add up to , so we have:
As triangle is half of a square, angles and are both . Together with the fact that triangles and are isosceles, this means that we have:
Hence angle .
From this the desired angle can be easily calculated, since angle and angle is a right-angle. Therefore angle is as angles in a triangle add up to and so angle as angles on a straight line also add up to .
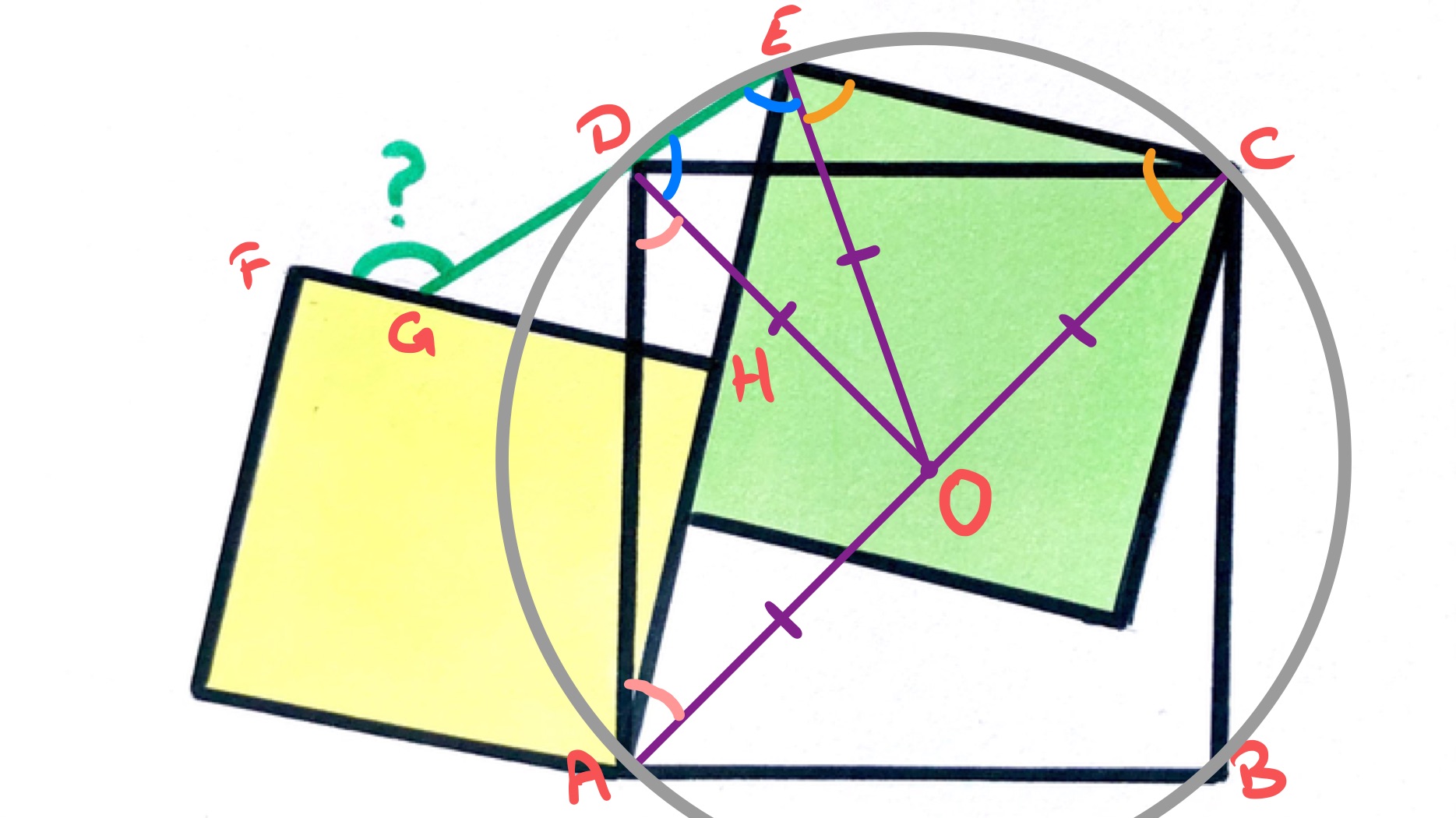
Solution by Circles
The triangle is a right-angled triangle with hypotenuse . Mark a point at the midpoint of . Then the circle centre with diameter also goes through .
The triangle is also a right-angled triangle with hypotenuse . So the same circle also goes through .
There are now two routes to get angle .
One route notes that is a cyclic quadrilateral and so . Since , this shows that and so .
The other route uses the chord with angles in the same segment to see that .
To get angle , we then note that so and so .