Notes
three squares and two triangles solution
Solution to the Three Squares and Two Triangles Puzzle
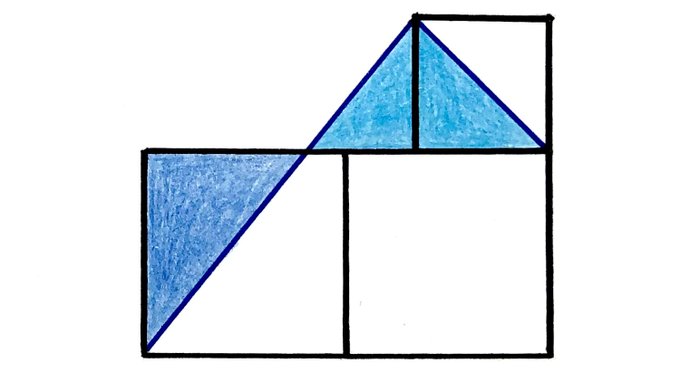
The two coloured triangles each have area 9. What’s the total area of the three squares?
Solution by Similar Triangles, Area of a Triangle, and Parallel Lines
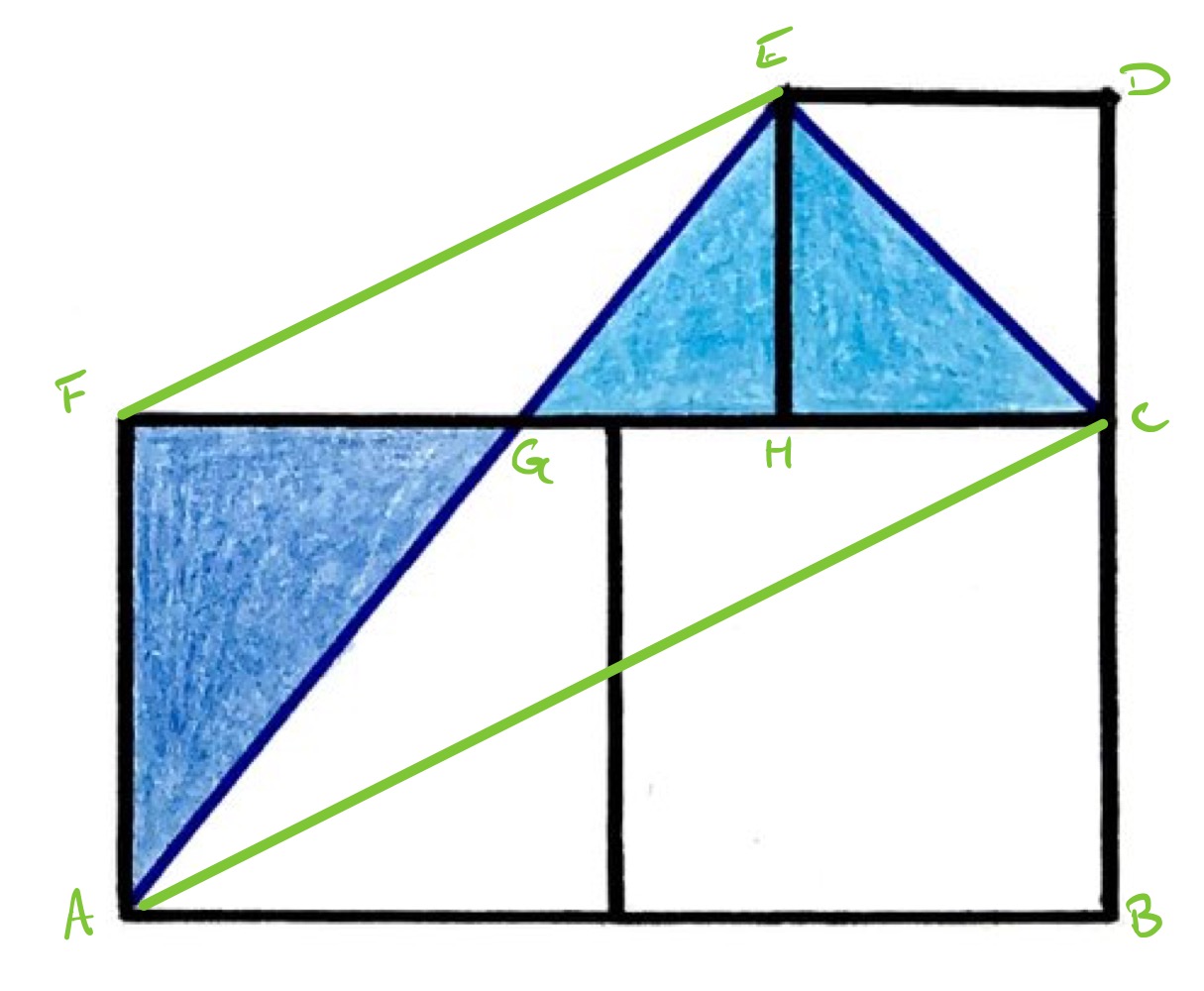
With the points labelled as above, consider triangles and . Triangle consists of triangles and , while triangle consists of triangles and . Since triangles and have the same area, so also do triangles and . Taking as the base of each, their heights above must therefore be the same. This means that the perpendicular distance from to is the same as that from , so is parallel to .
Since is also parallel to , this means that triangles and are similar. Therefore, the ratio of the length of to that of is . Since has the same length as , this means that divides in the ratio and so the side length of the smaller square is two thirds that of the larger.
Therefore, the length of is two thirds that of , and so since triangles and have the same area, the length of must be two thirds that of . The ratio of to is therefore . The area of triangle is therefore times that of , hence is .
The area of triangle is then , so the area of the two larger squares is .
The smaller square has side length that of the larger, so its area is of the larger, which is .
The area of the three squares is therefore .