Notes
three squares and an equilateral triangle solution
Solution to the Three Squares and an Equilateral Triangle Puzzle
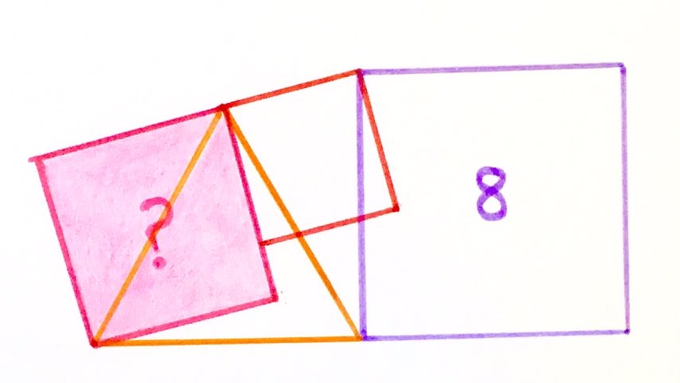
Three squares and an equilateral triangle. What’s the area of the pink square?
There is a hidden assumption here that the lower edge is a straight line.
Solution by Angles in a Triangle, Isosceles Triangles, and Lengths in a Square
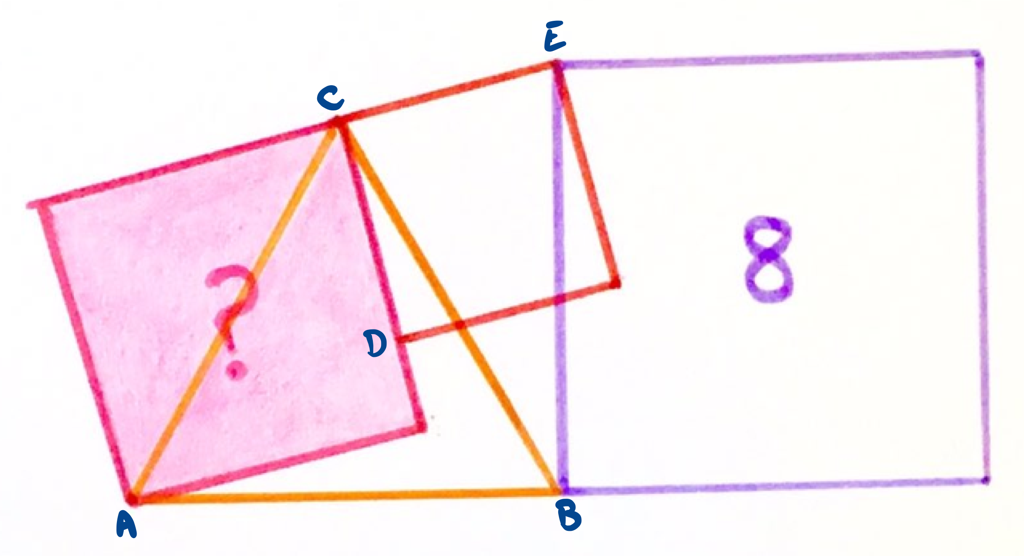
With the points labelled as above, angle and angle , so angle . Then since angle , angle .
Angle and angle , so angle . Then angle . Thus triangle is isosceles.
This means that and are the same length, then also and are the same length. So the side length of the right-hand square is the same length as the diagonal of the pink square.
The area of the pink square is therefore half the area of the right-hand square, thus is .