Notes
three squares and a triangle solution
Solution to the Three Squares and a Triangle Puzzle
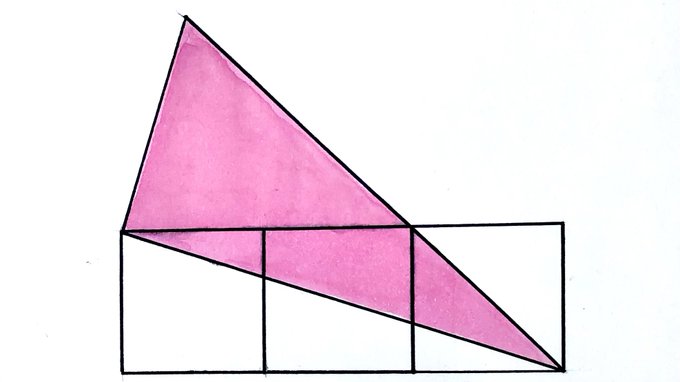
Each square has area 4. What’s the area of the pink right-angled triangle?
Solution by Similar Triangles and Area of Rectangles and Triangles
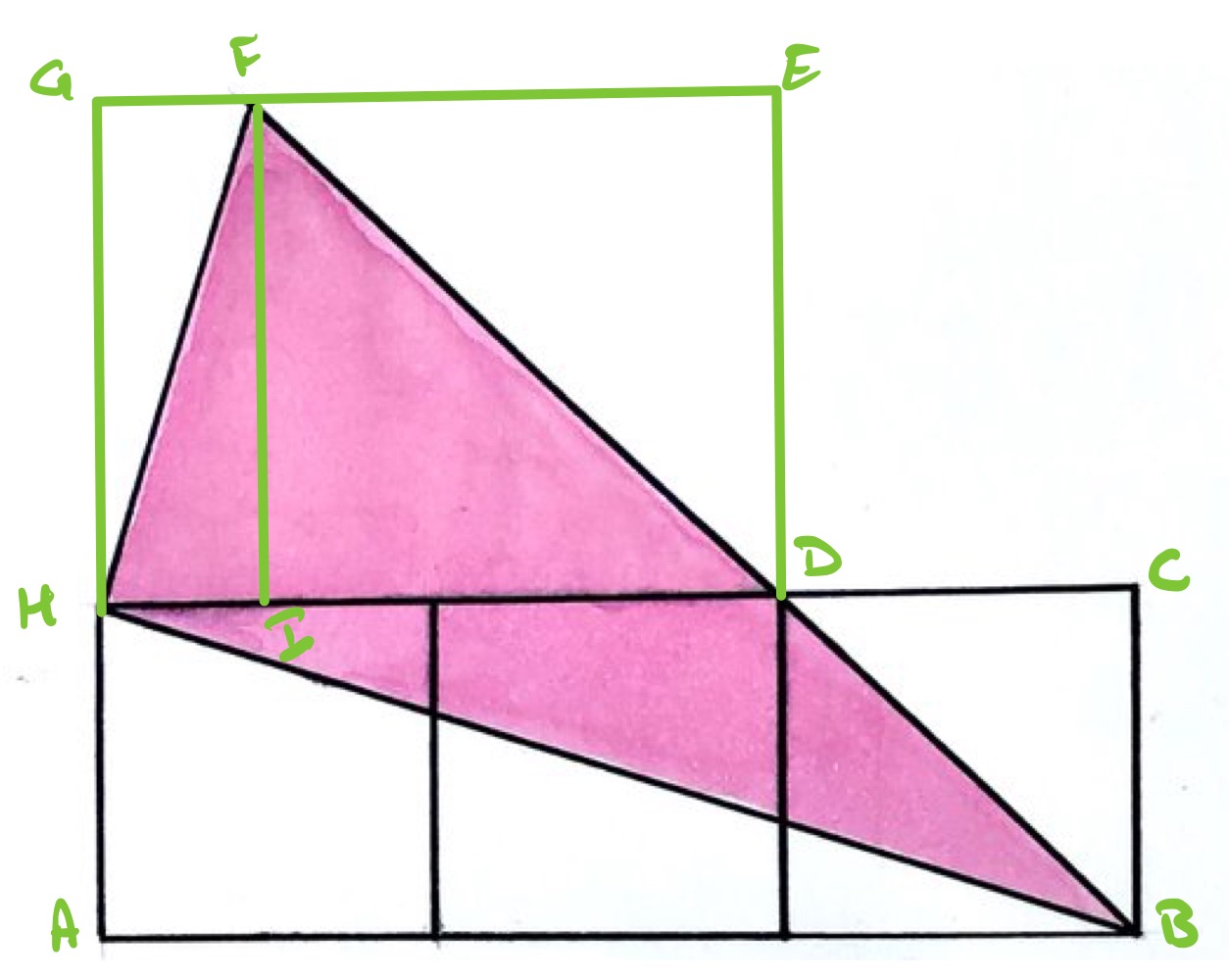
Label the points as above, where is such that is perpendicular to . As each square has area , the side lengths are .
Since the pink triangle is right-angled, angles and add up to , meaning that triangles and are similar. This shows that the lengths of the line segements and are in the ratio .
Since is the diagonal of a square, and it continues through to then is also a square. Therefore, line segments and are the same length. Therefore, splits into the ratio . Since has length , this means that has length and has length .
The original three squares have area . Rectangle has area . So the outer shape has area . The four white triangles have the following areas:
- :
- :
- :
- :
So the pink triangle has area: