Notes
three squares and a semi-circle solution
Solution to the Three Squares and a Semi-Circle Puzzle
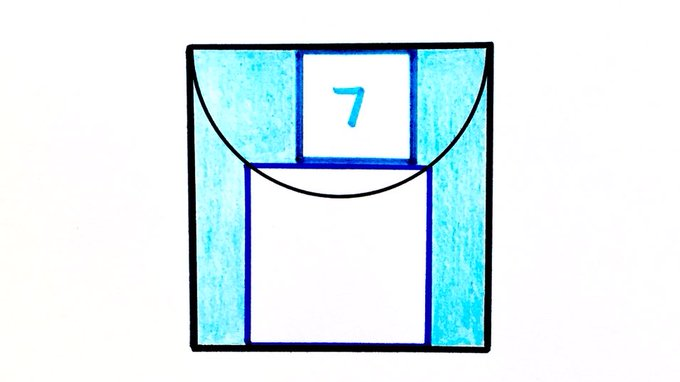
The smallest of these three squares has area . What’s the total shaded area?
Solution by Properties of Chords and Pythagoras' Theorem
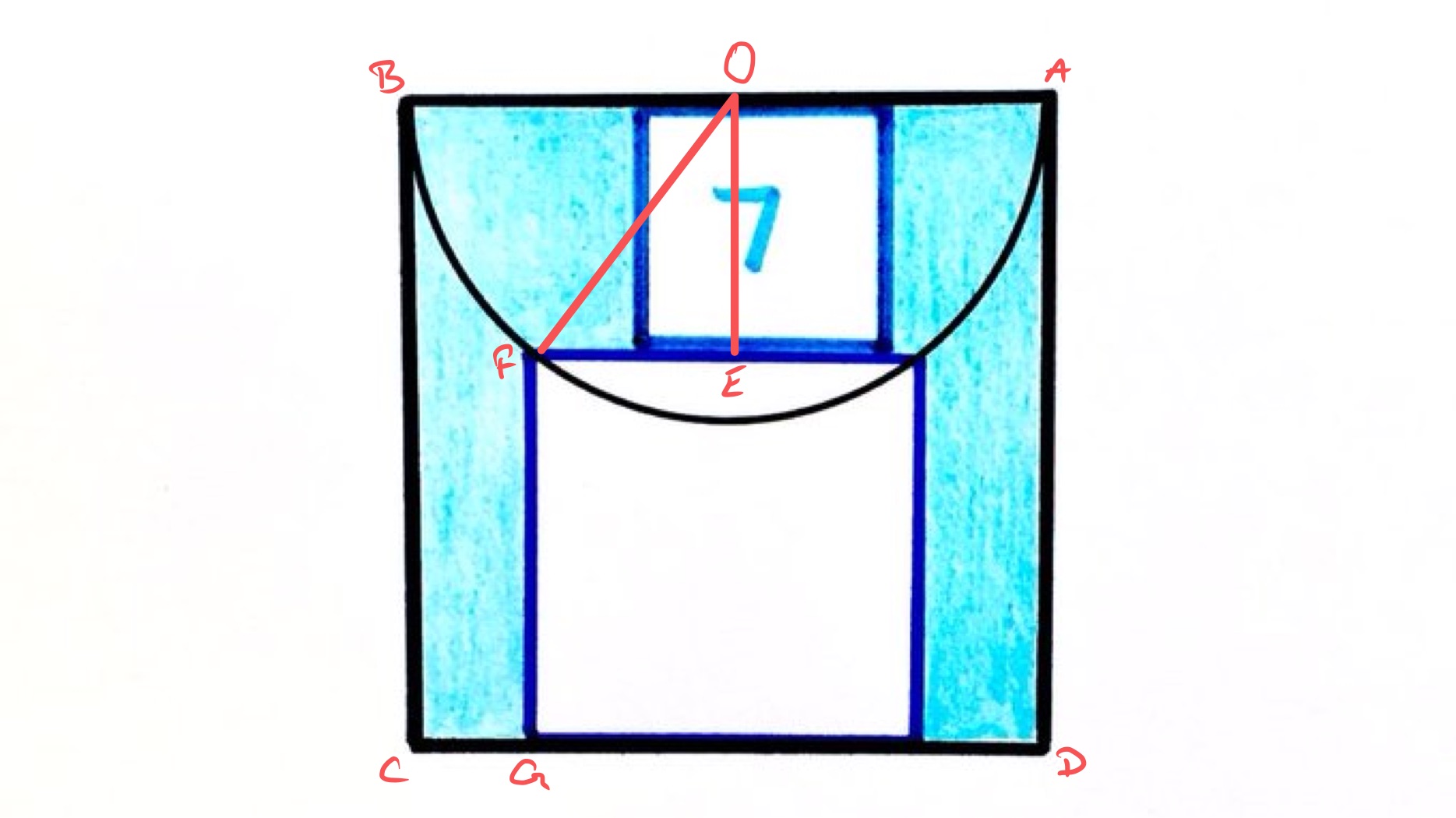
In the diagram above, the point labelled is the centre of the semi-circle.
Let the squares have side lengths , , and in increasing order, so that . The area of the shaded region is .
As one of the sides of the middle square forms a chord across the circle, is half of that side and is perpendicular to . Therefore triangle is right-angled and has side lengths , , and . Applying Pythagoras' theorem shows that:
Then the shaded region has area .