Notes
three squares and a rectangle solution
Solution to the Three Squares and a Rectangle Puzzle
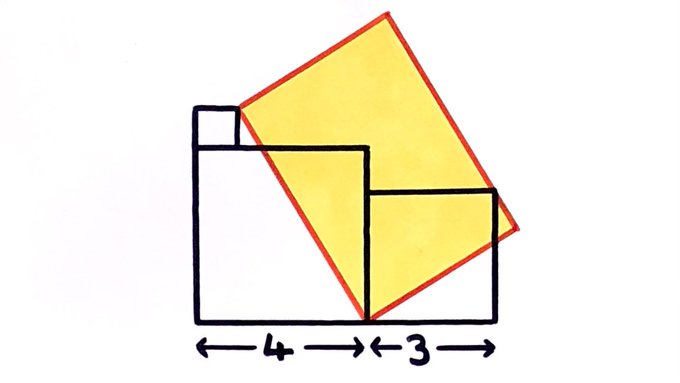
Three squares and a rectangle. What’s the shaded area?
Solution by Similar Triangles and Lengths in a Square
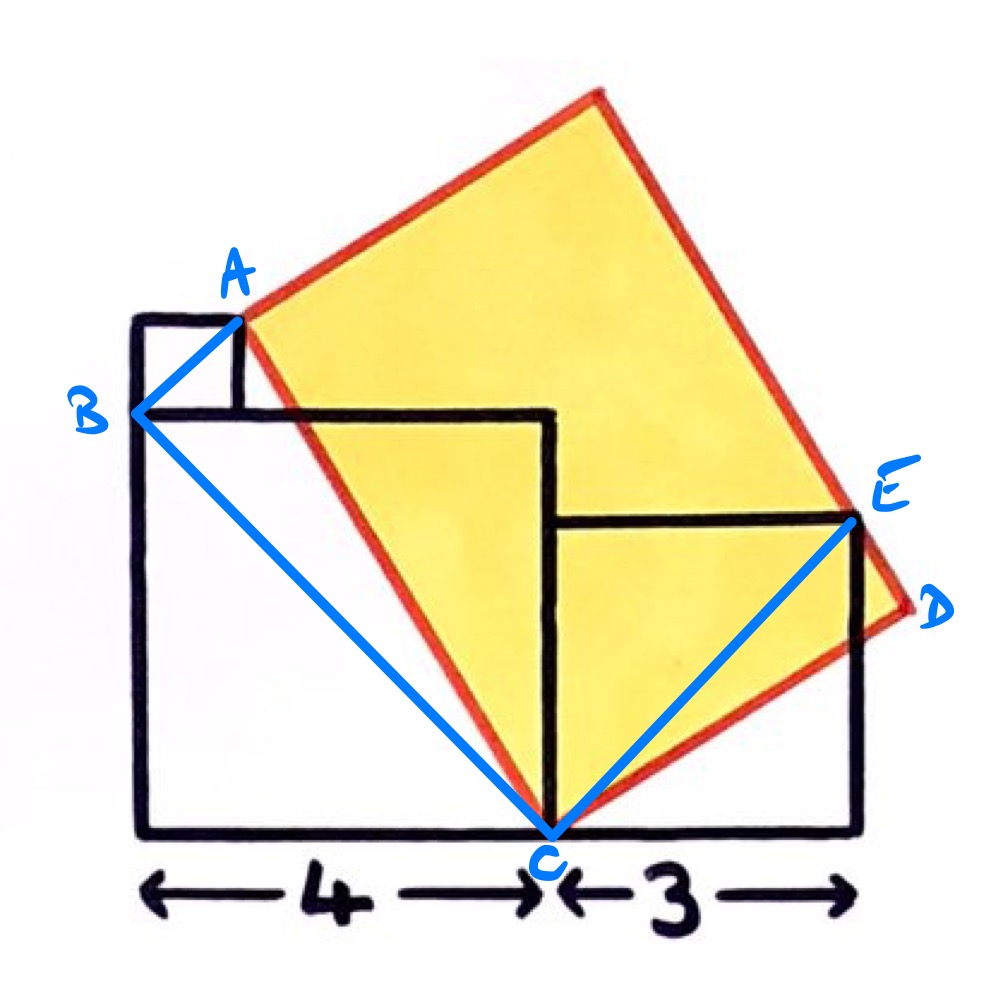
Consider the diagram as labelled above. In this diagram, triangles and are right angled and angle is equal to angle since each together with angle make a right-angle. Therefore, triangles and are similar.
This means that the ratios and are equal. So the lengths satisfy:
Multiplying up gives:
Then is the diagonal of a square of side length , and of , so has length while has length . Hence
Solution by Invariance Principle
The tilt of the shaded rectangle is not specified, allowing a range of angles with two special cases.
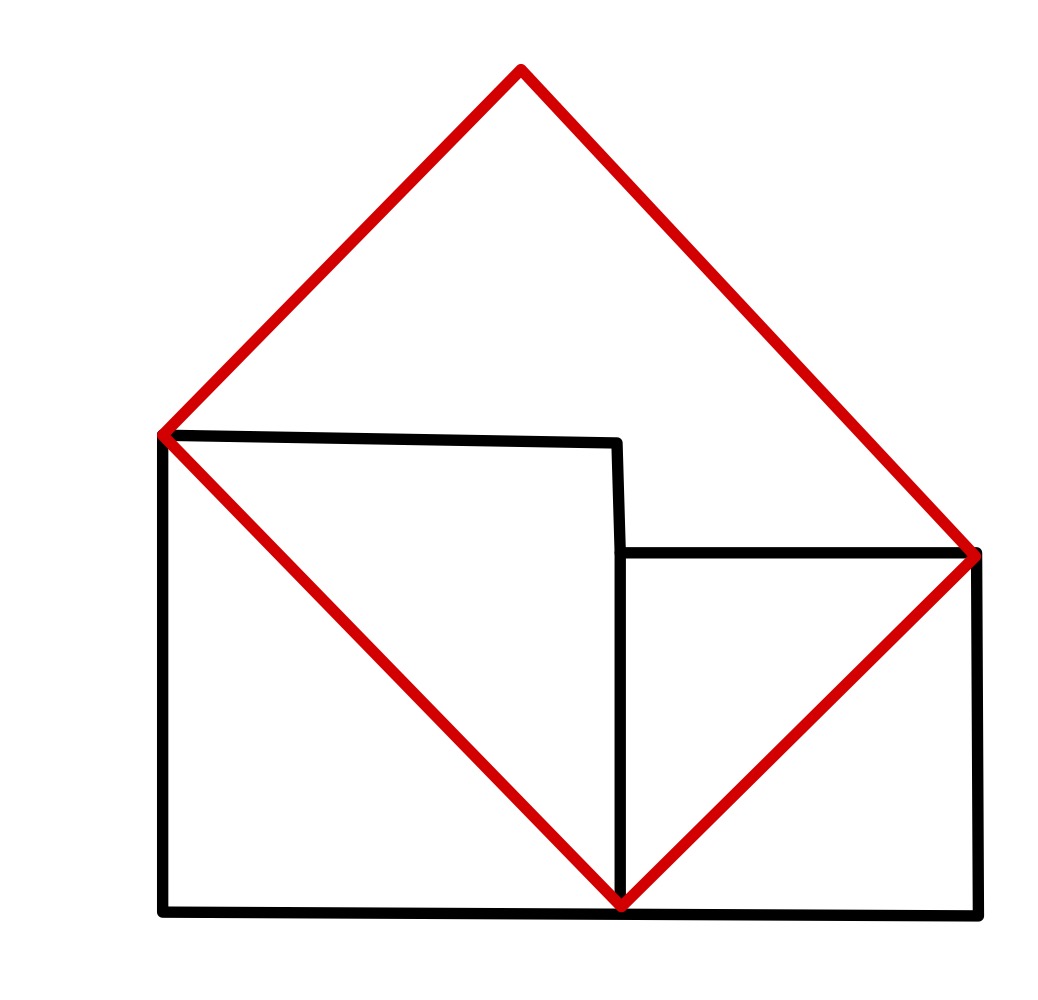
In this configuration, the small square is shrunken to a point meaning that the sides of the rectangle are the diagonals of the squares. So the area is .
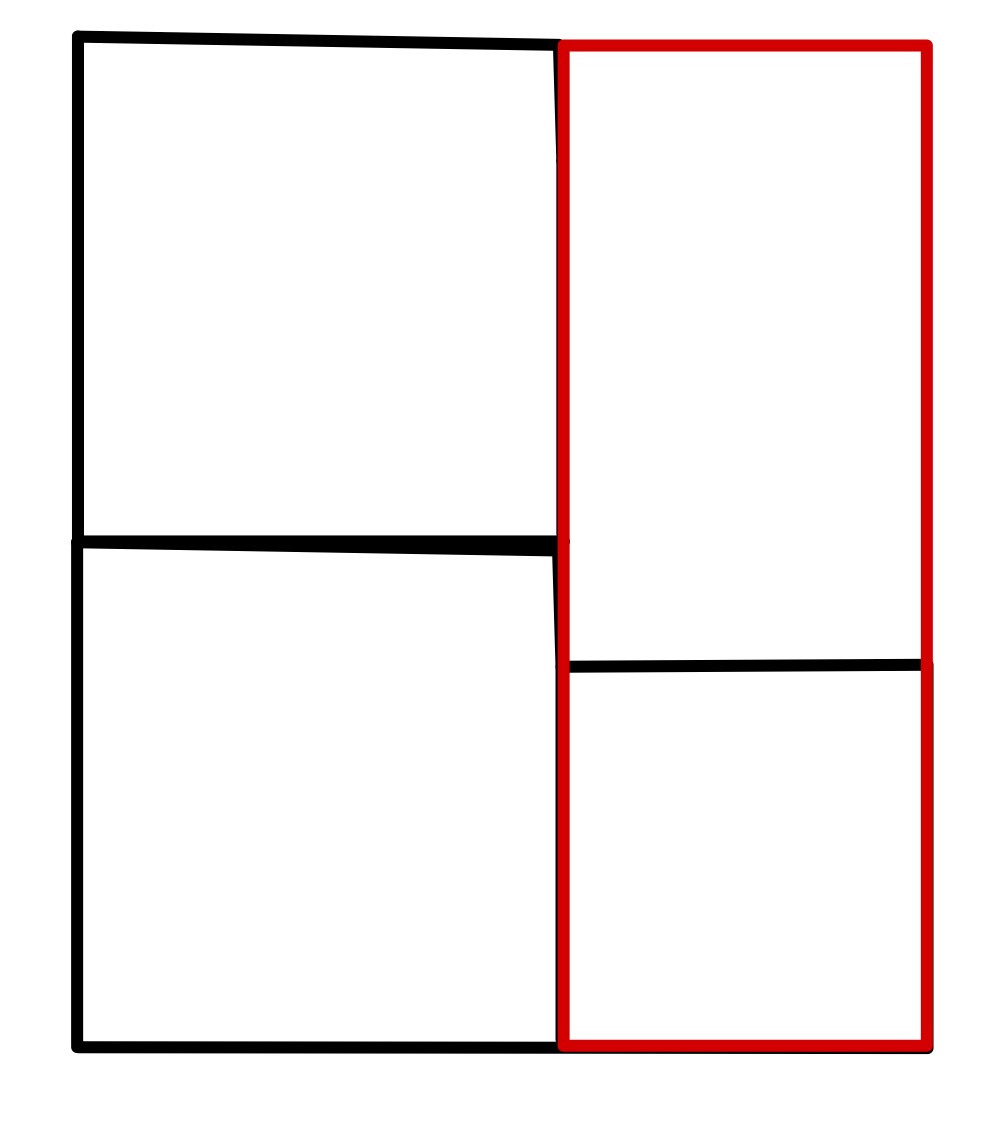
In this configuration, the small square is the same size as the square of side length , meaning that the shaded rectangle has sides and so area .