Notes
three semi-circles solution
Three Semi-Circles
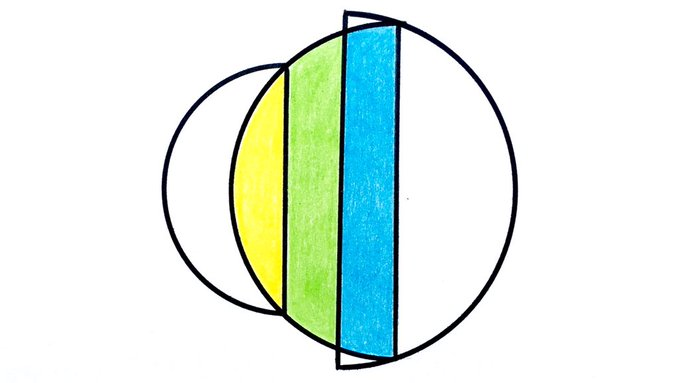
The three coloured stripes are each the same width. If the smallest semicircle has area , what’s the area of the largest?
Solution by Pythagoras' Theorem and Circle Area
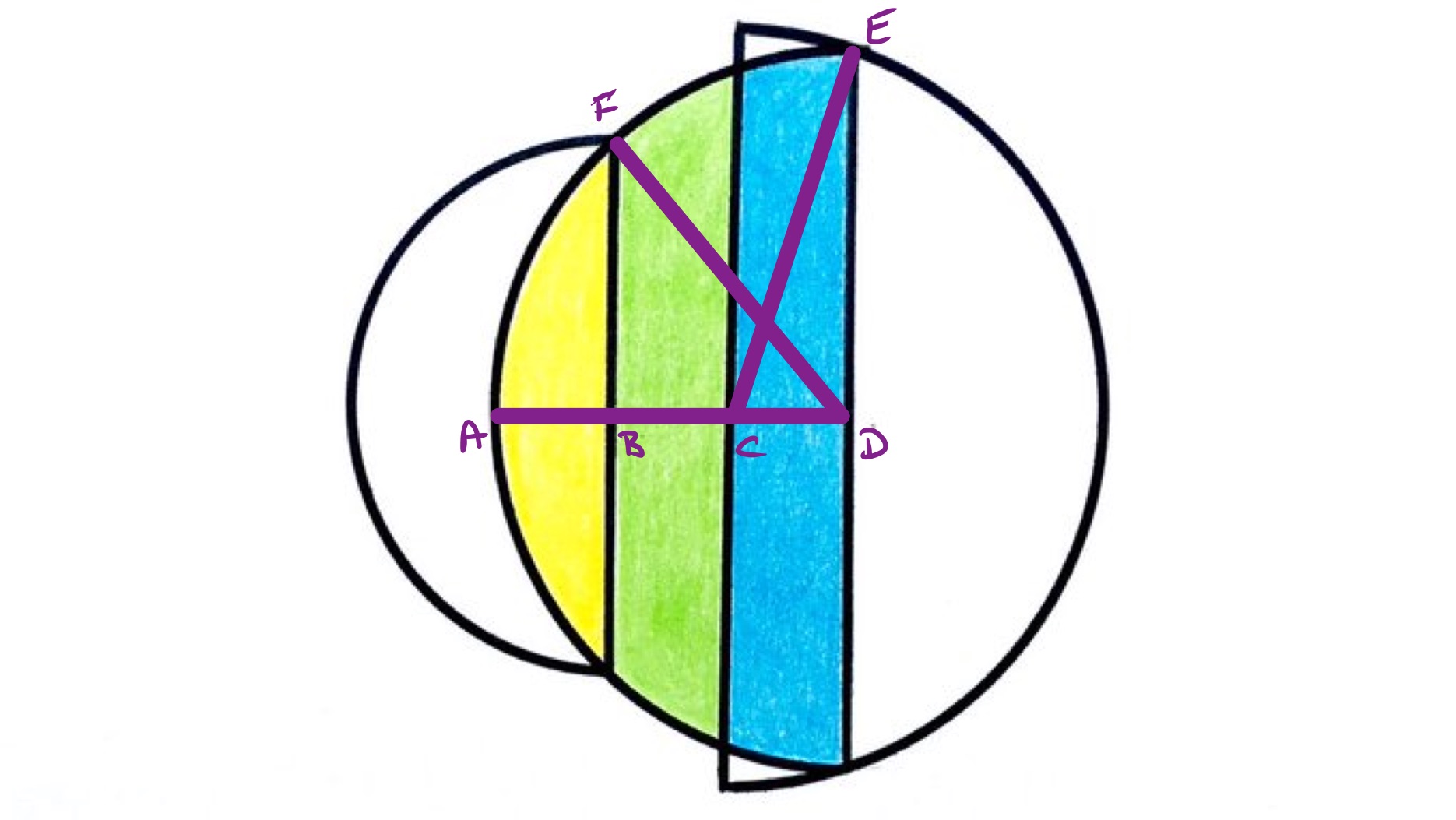
Let , , be the radii of the three semi-circles in increasing order. With the points labelled as above, then is the length of , of and , and of . Each of , , and are one third of the radius of the middle semi-circle, so are .
Applying Pythagoras' theorem to triangle gives the relationship:
so .
Applying Pythagoras' theorem to triangle gives the relationship:
so .
The area of the larger semi-circle is . The area of the smallest semi-circle is , which is , so the largest semi-circle has area .