Notes
three semi-circles around a triangle solution
Solution to the Three Semi-Circles Around a Triangle Puzzle
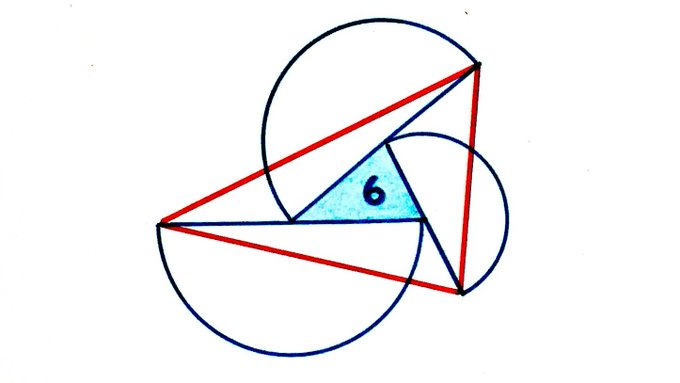
What’s the area of the red triangle?
Solution by Area of a Triangle
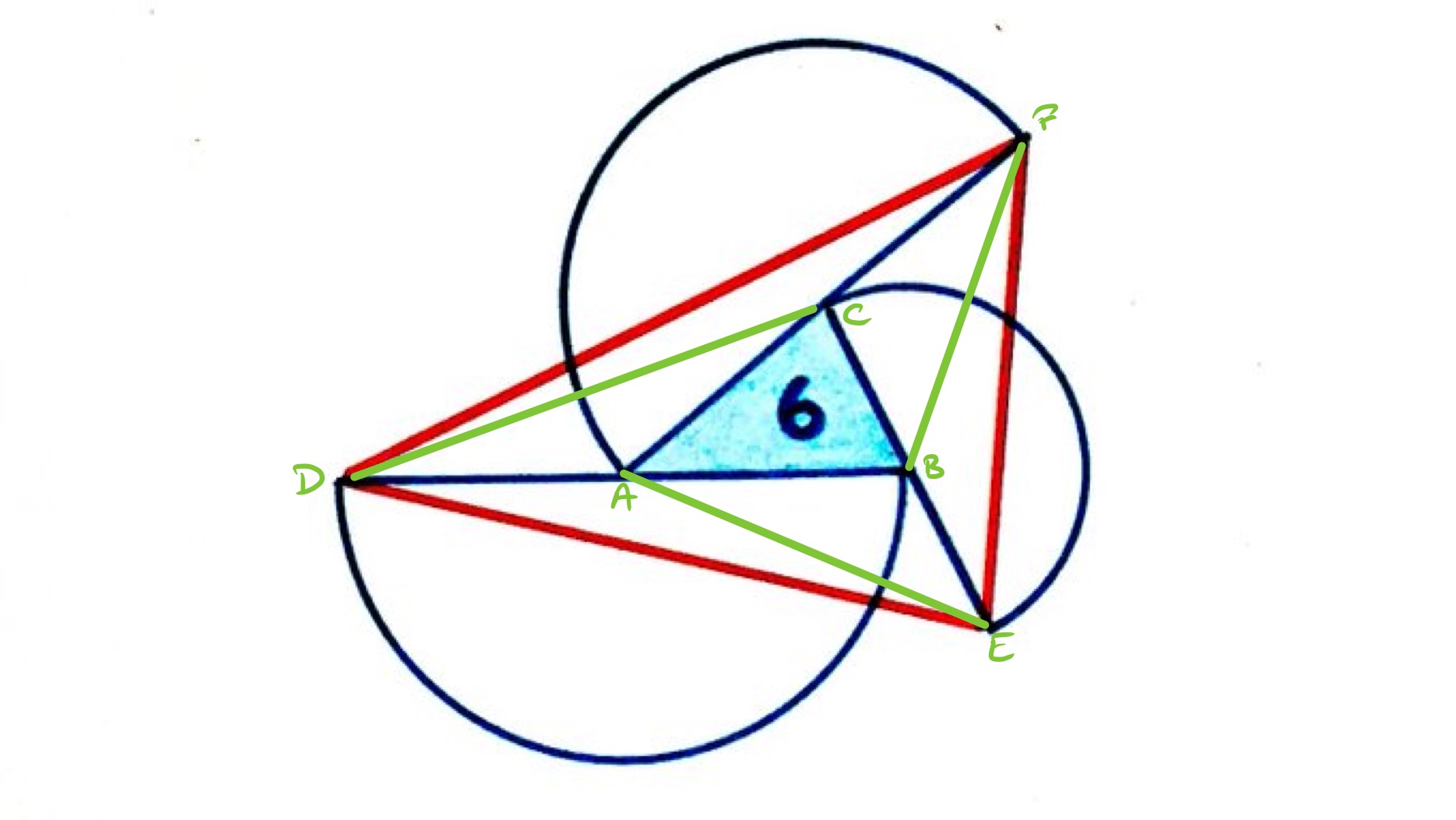
The decomposition shown in the above diagram splits the red triangle into seven regions. Other than the central one, the regions can be paired up with triangles and comprising one pair and continuing this around the central triangle.
That triangles and have the same area comes from the fact that and are radii of the same semi-circle so have the same length, and then the triangles share as apex above this line. Then is the same length as as both are radii of another semi-circle, and they are the same perpendicular distance from (albeit on different sides). Therefore triangles and have the same area.
This argument continues round the pairs, showing that each of the extra triangles has the same area as the central one. The area of the red triangle is therefore .