Notes
three quarter circles solution

Solution to the Three Quarter Circles Puzzle

Solution by Similar Triangles and Angles in a Triangle

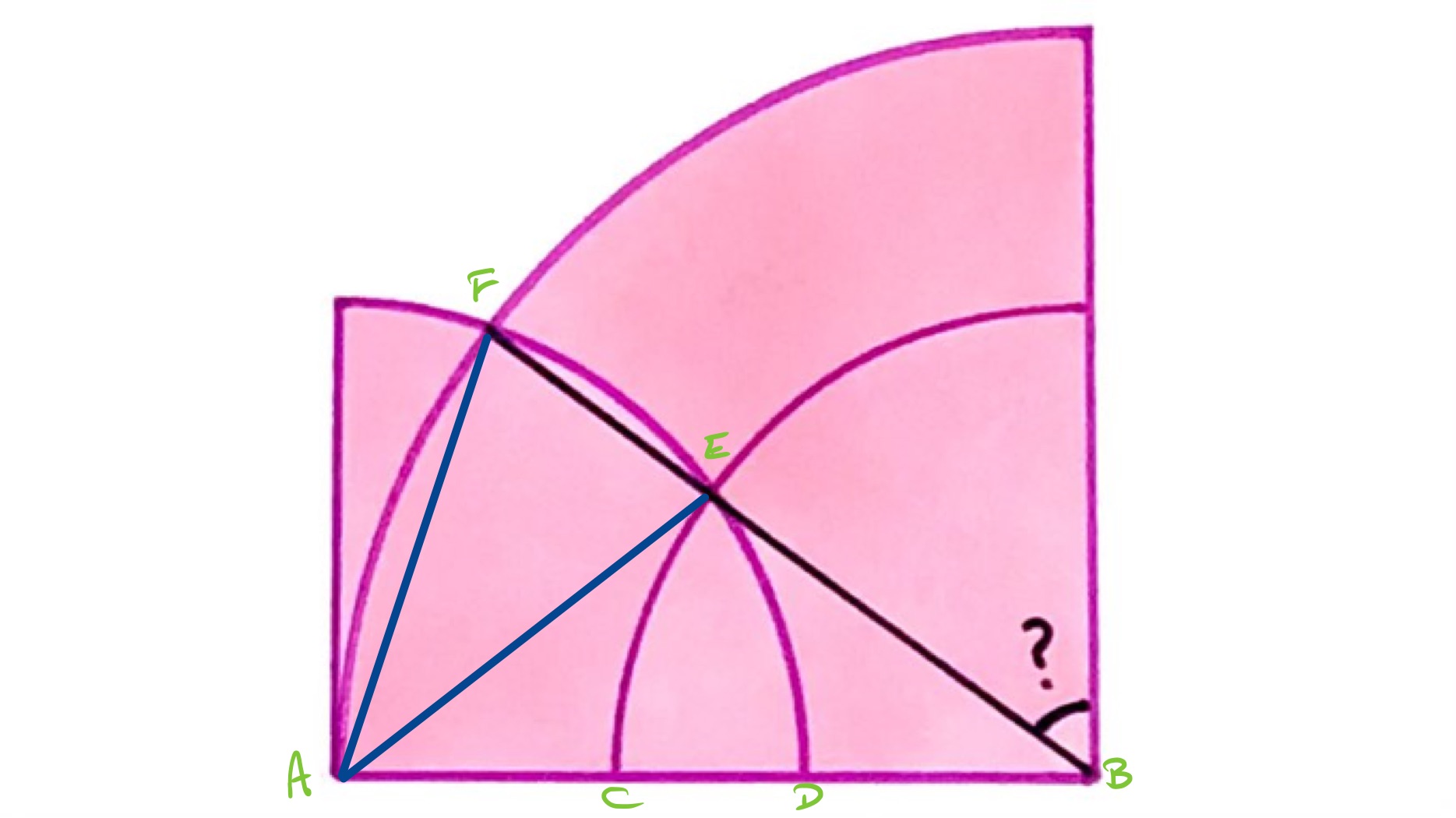
With the points labelled as in the diagram, the following line segments are all radii of one or other of the two quarter circles that are the same size and so all have the same length: $A F$, $A E$, and $B E$. Therefore triangles $A E F$ and $E A B$ are isosceles. Triangle $B F A$ is also isosceles as the line segments $B F$ and $B A$ are radii of the larger quarter circle.

The triangles $A E F$ and $B F A$ share an angle at $F$, and this is a “base” angle for both isosceles triangles so these triangles are similar. Therefore angle $F \hat{A} E$ is equal to angle $F \hat{B} A$ and thus also to angle $E \hat{A} B$. The base angle of triangle $B F A$ is therefore twice the apex angle, and so the sum of the angles in triangle $B F A$ is five times the angle $F \hat{B} A$. Since the sum of the angles in a triangle is $180^\circ$, angle $F \hat{B} A$ is therefore $\frac{180^\circ}{5} = 36^\circ$.

The requested angle is thus $90^\circ - 36^\circ = 54^\circ$.