Notes
three parallel semi-circles solution

Solution to the Three Parallel Semi-Circles Puzzle

Solution by Pythagoras' Theorem and Area of a Circle

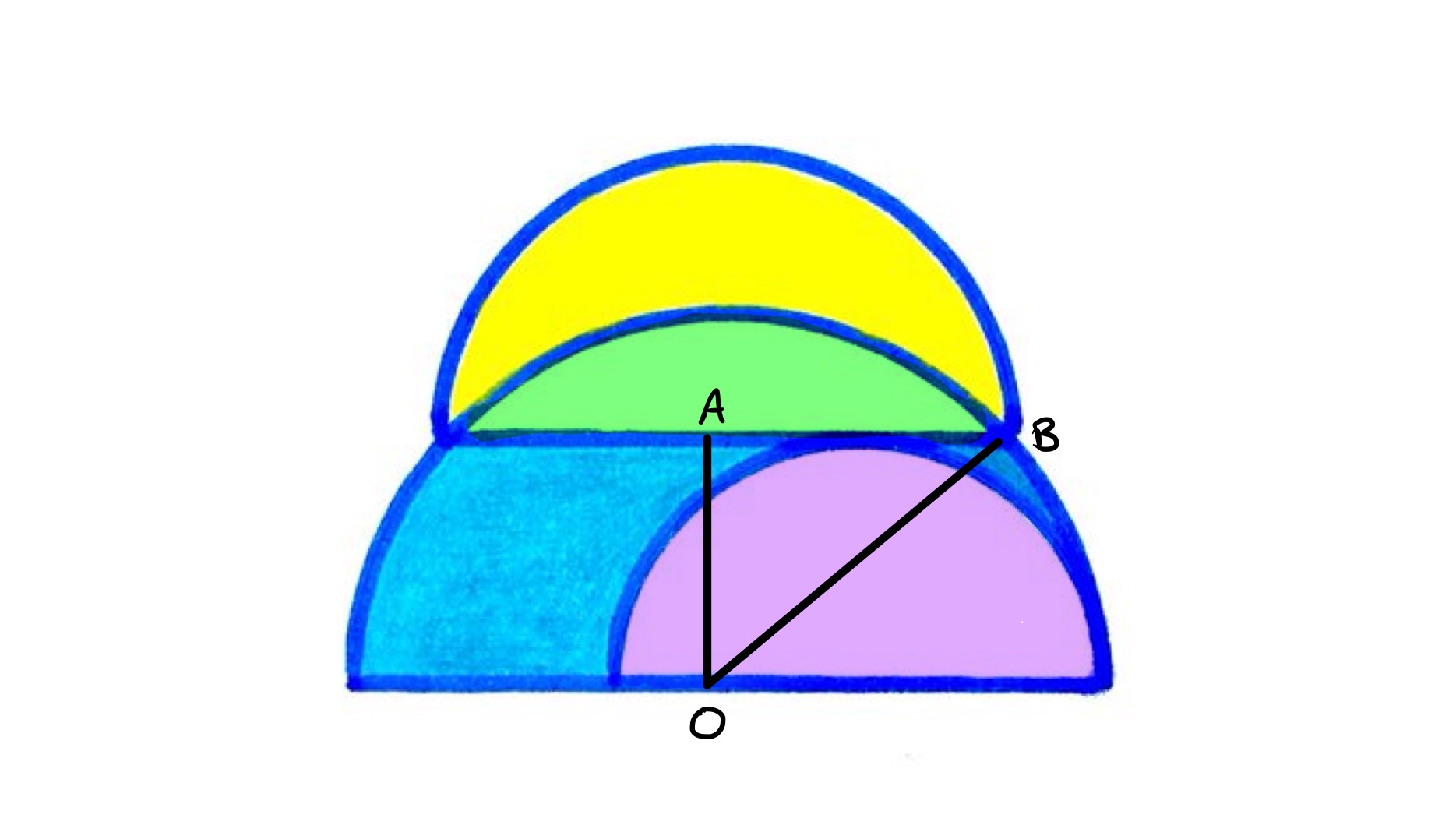
In the above diagram, the point labelled $O$ is the centre of the largest semi-circle and $A$ of the middle one. Triangle $O A B$ is right-angled since the perpendicular bisector of a chord passes through the centre of the circle. Let $c$ be the length of $O B$, $b$ of $A B$, and $a$ of $O A$. Then by Pythagoras' theorem $c^2 = a^2 + b^2$.

The line segment $O A$ is the same length as the radius of the smallest semi-circle, so the area of the largest semi-circle without the smallest is given by:

so is the same as the area of the middle semi-circle.

The middle semi-circle comprises the yellow and green regions, while the largest without the smallest comprises the blue and green regions. Since these combined regions are the same area, the yellow and blue regions must have the same area. The total blue area is therefore also $6$.