Notes
three overlapping semi-circles solution
Solution to the Three Overlapping Semi-Circles Puzzle
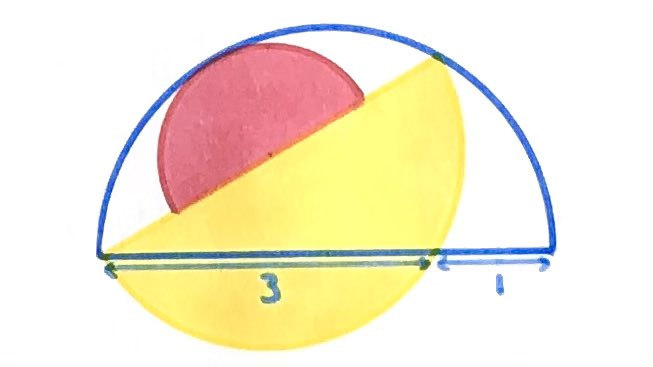
What’s the total shaded area?
Solution by Angle in a Semi-Circle and Pythagoras' Theorem
ThreeOverlappingSemiCirclesLabelled.png
In the diagram above, is the point where the yellow semi-circle intersects the diameter of the blue. As is a diameter of the yellow semi-circle, using angle in a semi-circle, angle is a right-angle and so triangle is a right-angled triangle.
The point is the centre of the blue circle, so and are both radii and so are of length . Therefore, is the midpoint of . Since is directly above , it is equidistant from and and so triangle is isosceles with and of the same length. Since also and have the same length, is therefore equilateral.
Point is both the centre of the red semi-circle and the midpoint of . Triangle is an isosceles triangle with angle , since triangle is equilateral. Cutting along creates two right-angled triangles that can be reassembled into an equilateral triangle, demonstrating that is half of . Therefore also is the same as .
As the triangle is a right-angled triangle, applying Pythagoras' theorem to it results in
The areas of the red and yellow semi-circles are given by
Putting these together, and using the fact that has length , the shaded area is
Note: is half of which has length so has length , it is also possible to show that is without using Pythagoras’ theorem, see equilateral triangle for the details, so the shaded area is and this does not use Pythagoras’ theorem.