Notes
three overlapping rectangles ii solution
Three Overlapping Rectangles II
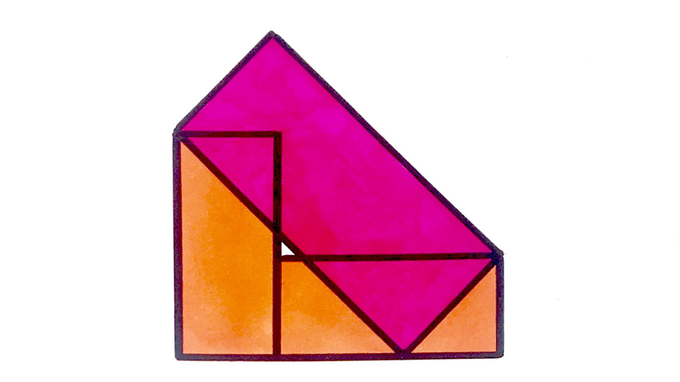
The two small rectangles are congruent and each have area . What’s the area of the large rectangle?
Solution by Similar Triangles
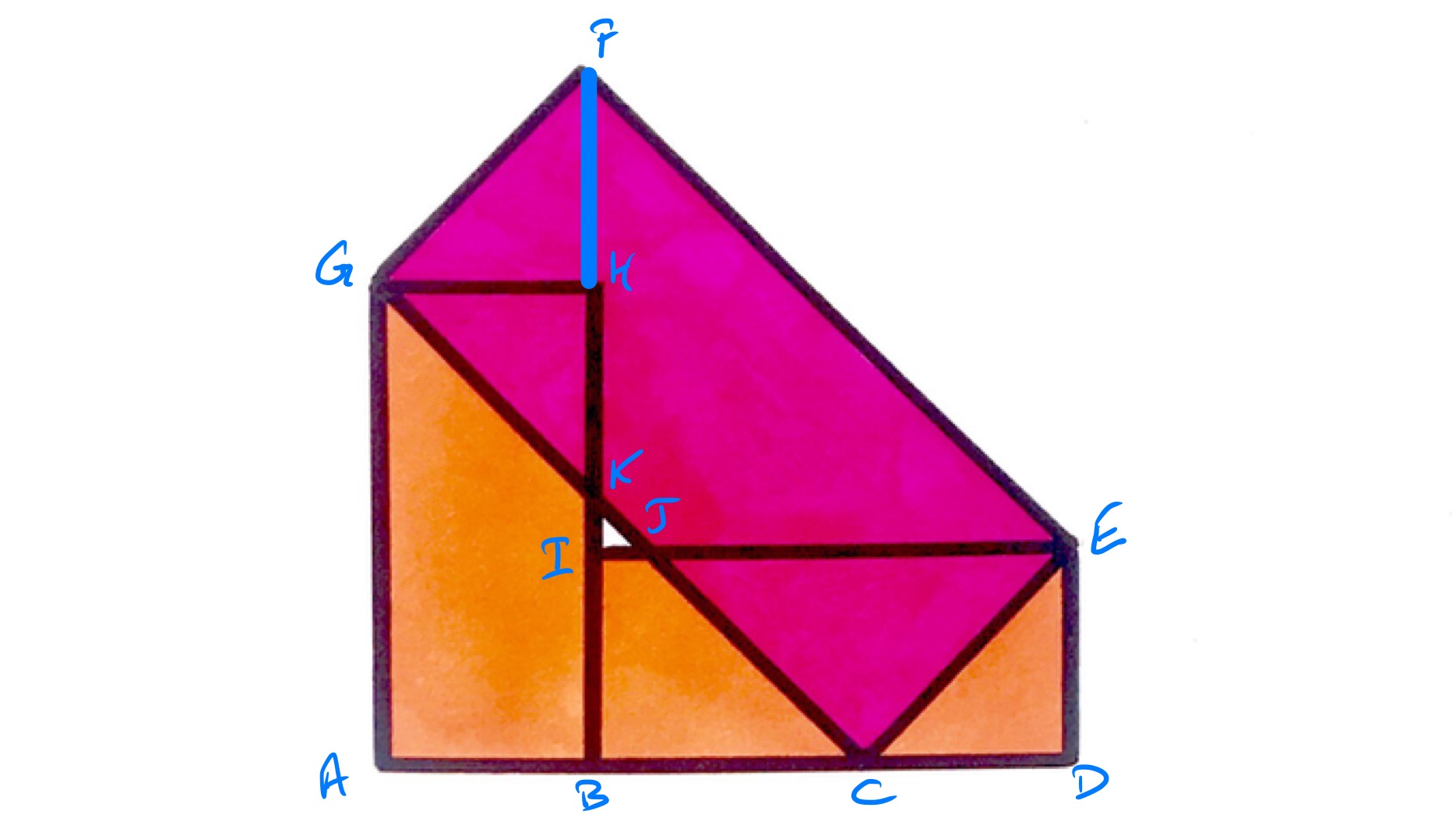
With the points labelled as in the above diagram, let and be the lengths of the sides of the orange rectangle, with the length of and the length of .
The triangles and are similar, with corresponding to , because they are both right-angled triangles and the angles and add up to using angles on a straight line.
Let be the length of and of . Then the ratios and are equal, meaning that . Then also the length of is and , so these are also equal. This is enough to show that and are equal to and in some order, and from the diagram it must be that and .
(This can also be seen using circle geometry. Draw a circle centred on the midpoint of the line segment joining with as diameter. Since angle is a right-angle - this is because the rectangles are similar so their diagonals are at right-angles - the point lies on this circle. Since also angle is a right-angle, the point also lies on this circle. Then by symmetry, the lengths of and are equal.)
This then shows that the triangles and are isosceles right-angled triangles, and so the length of is while the length of is . So the area of the pink rectangle is .
Solution by Invariance Principle
The orange rectangles can be varied, providing their area remains . By drawing them as squares, as in the following diagram, the area of the pink rectangle (now also a square) is clearly the same as the total area of the orange squares, thus .