Notes
three lengths in a semi-circle solution
Solution to the Three Lengths in A Semi-Circle Puzzle
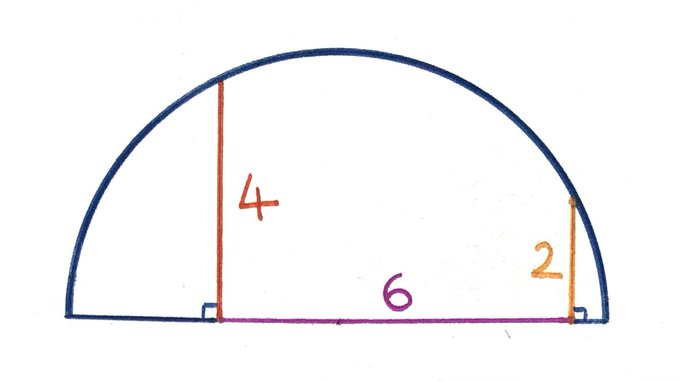
What’s the area of this semicircle?
Solution by Pythagoras' Theorem
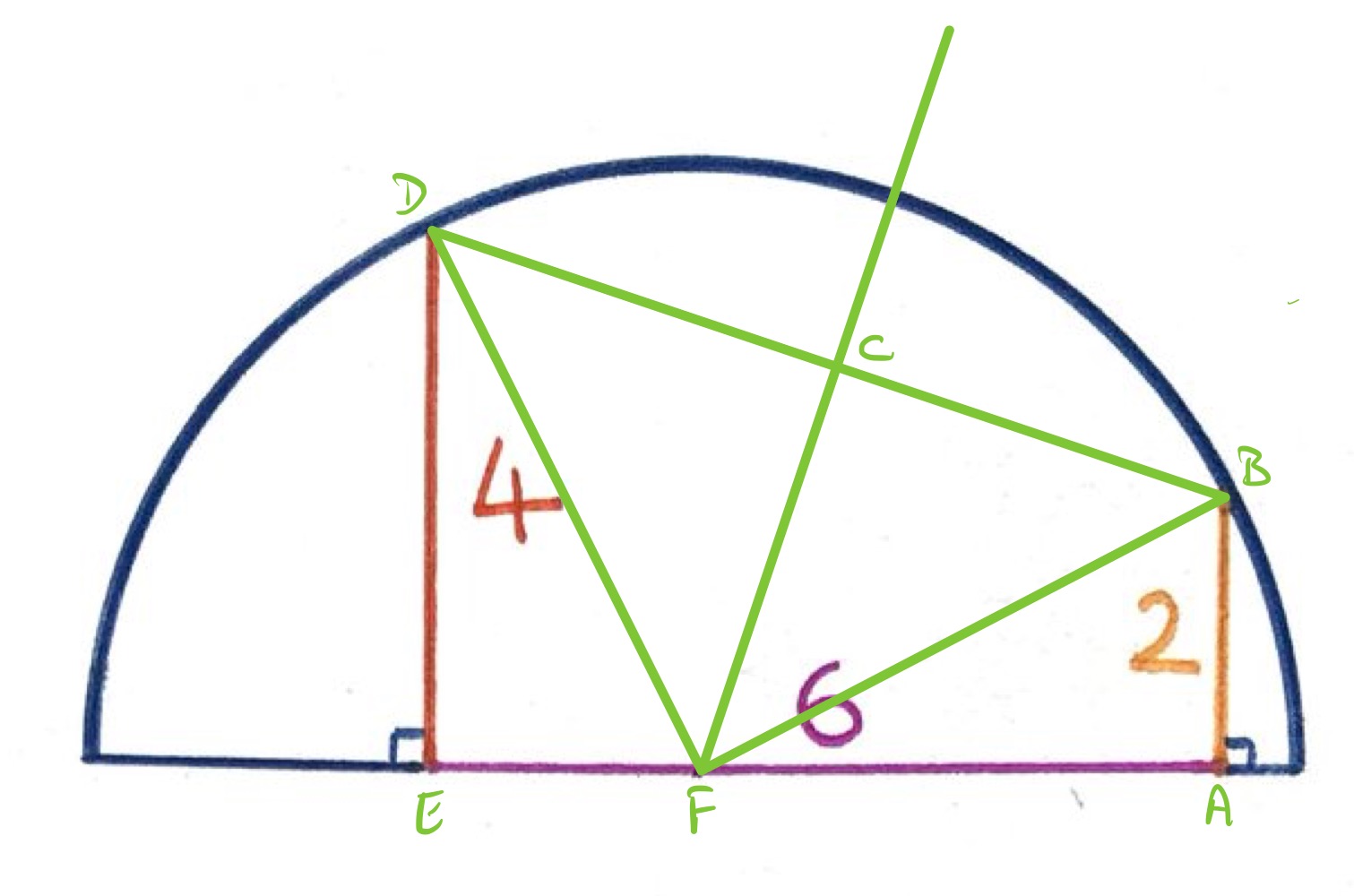
Consider the diagram as labelled above, in which is the centre of the semi-circle. Then triangles and are right-angled so Pythagoras' theorem applies. The line segments and are both radii of the semi-circle, so have the same length.
Let be the radius of the semi-circle and the length of the line segment , so line segment has length . Then Pythagoras' theorem says:
Subtracting these gives and so . Then . The area of the semi-circle is therefore .
Solution by Perpendicular Bisector of a Chord and Pythagoras' Theorem
In this version, the diagram is as above but is taken so that line segment has length and therefore line segment has length . Triangles and are therefore right-angled with two lengths the same, and hence are congruent. This means that and have the same length, so lies on the perpendicular bisector of chord . As it also lies on the diameter that goes through and , it must be the centre of the circle.
Therefore is a radius of the circle, and Pythagoras' theorem shows that it has length . The area of the semi-circle is therefore as before.