Notes
three isoscelese triangles inside a triangle solution
Three Isosceles Triangles Inside a Triangle
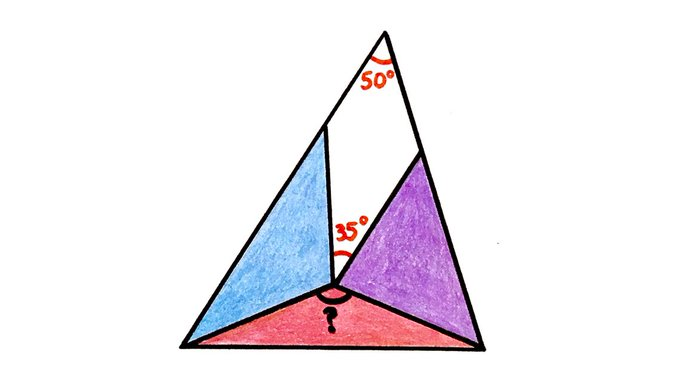
The three shaded triangles are isosceles. What’s the missing angle?
Solution by Angles at a Point, Angles on a Straight Line, Angles in a Triangle, Angles in a Quadrilateral
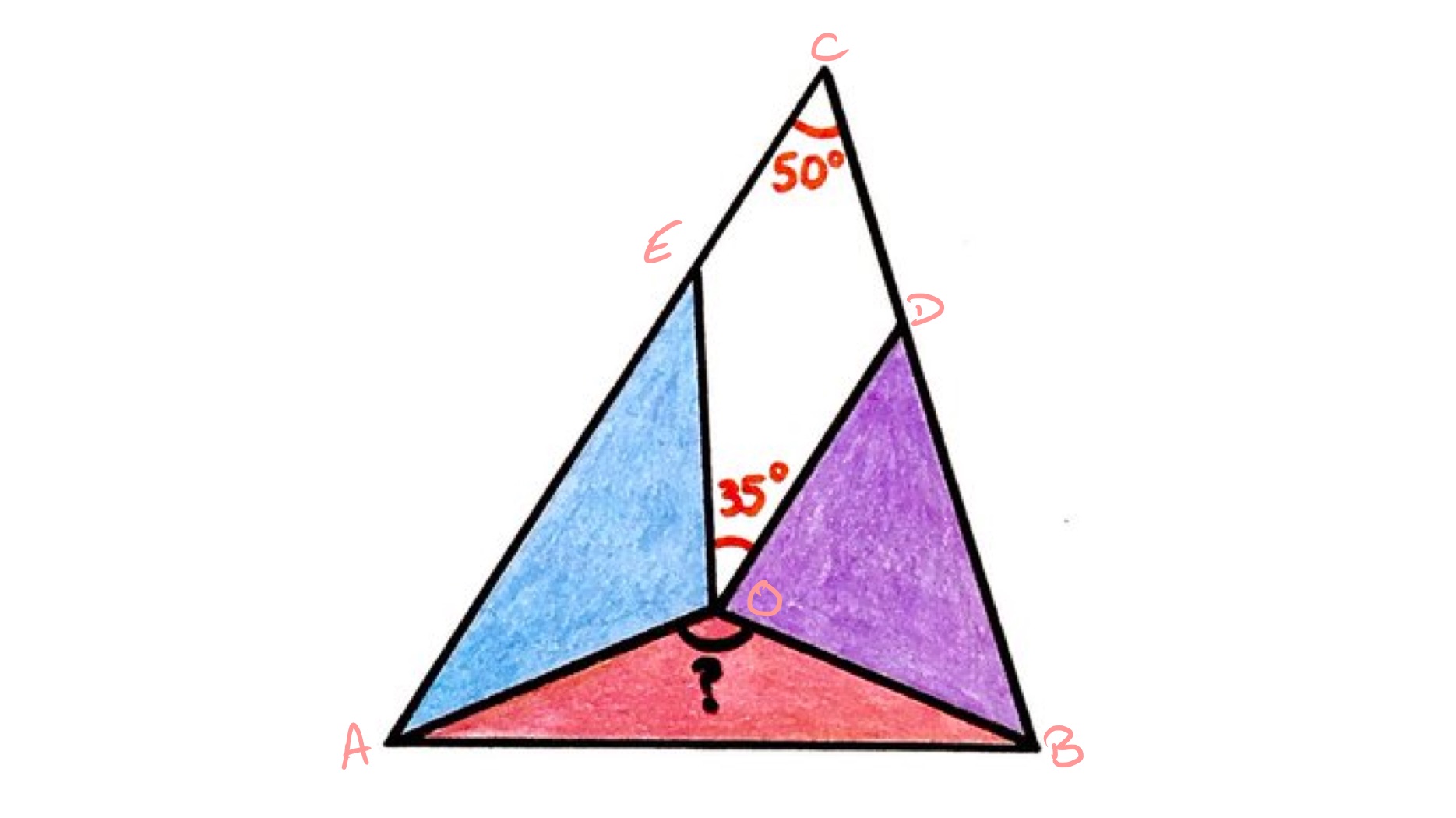
With the points labelled as in the diagram, let be angle , angle , and angle . Then as angles at a point add up to , .
Triangle is isosceles so angle is as angles in a triangle add up to . So since angles at a point on a straight line also add up to , angle is . A similar argument shows that angle is .
Since the angles in a quadrilateral add up to , considering quadrilateral gives the equation:
and this simplifies to . Hence .