Notes
three equilateral triangles and a semi-circle solution
Solution to the Three Equilateral Triangles and a Semi-Circle Puzzle
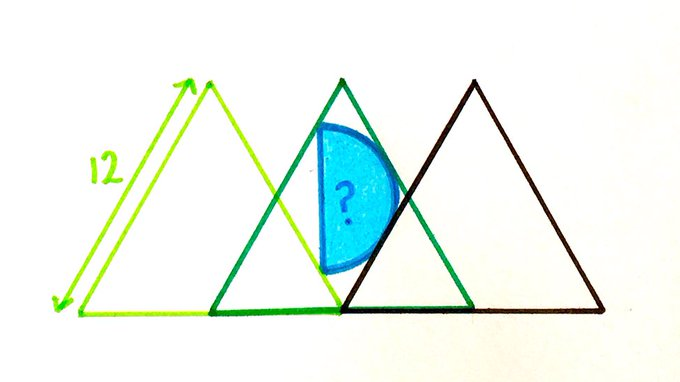
The three equilateral triangles have sides of length . What’s the area of the semicircle?
Solution by Lengths in Equilateral Triangles, Angle in a Semi-Circle
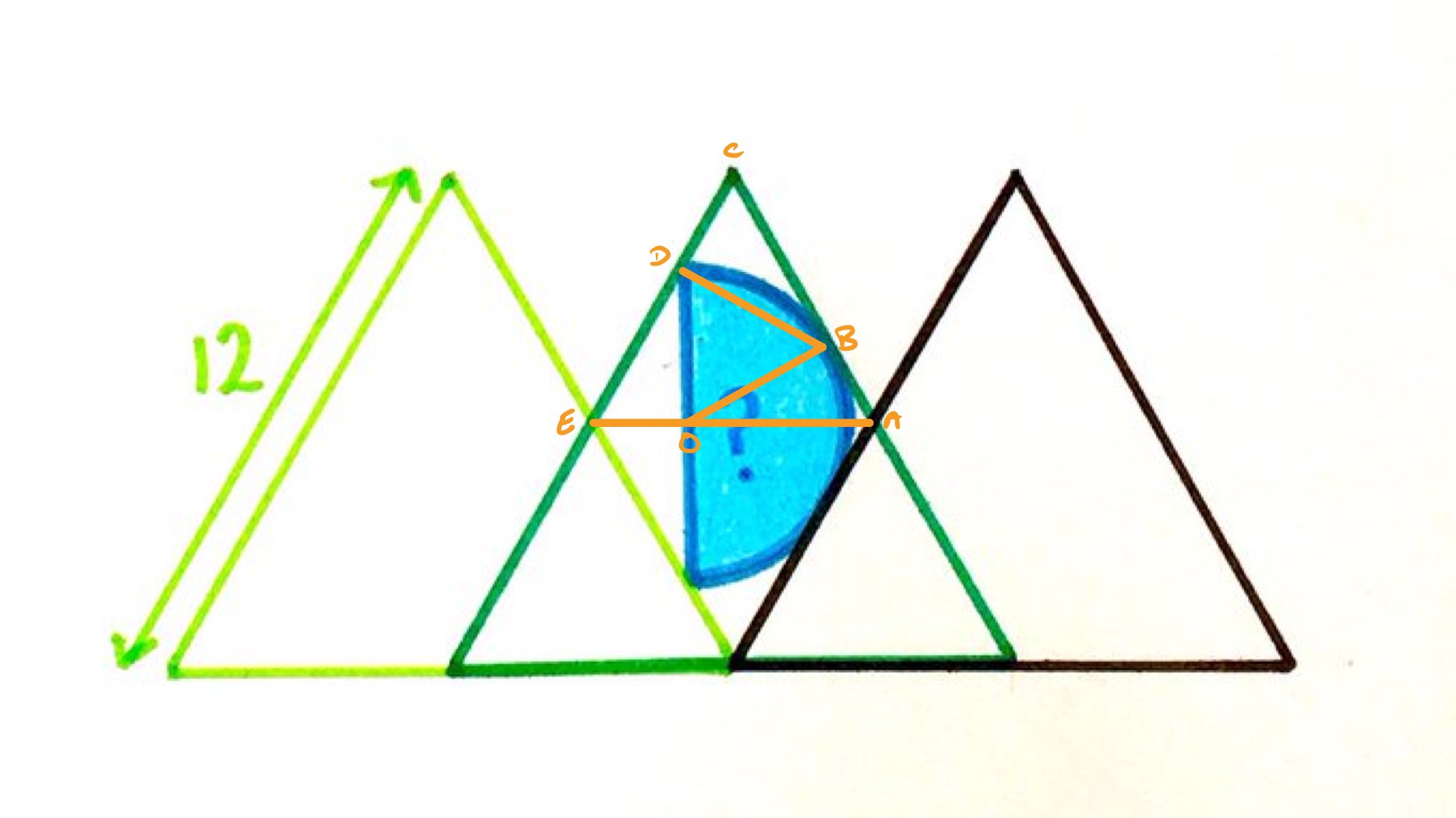
With the points labelled as in the diagram, the reflective symmetry of the semi-circle shows that the points and must be at the same height, which shows that the overlaps between the two pairs of triangles are equal. This means that is an equilateral triangle with side length .
The point is where the semi-circle meets , so angle is the angle between a radius and tangent which is . This means that triangle is right-angled. Since angle is the internal angle of an equilateral triangle, it is , meaning that angle is and so angle is again . As triangle must be isosceles, this shows that it is in fact equilateral.
Then triangles , , and are congruent and are half of an equilateral triangle. So the length of is half that of , and so of , meaning that has length . The length of is then times the length of , from lengths in an equilateral triangle, so is of length .
This is the radius of the semi-circle, so the area of the semi-circle is .