Notes
three equal area rectangles solution
Three Equal Area Rectangles
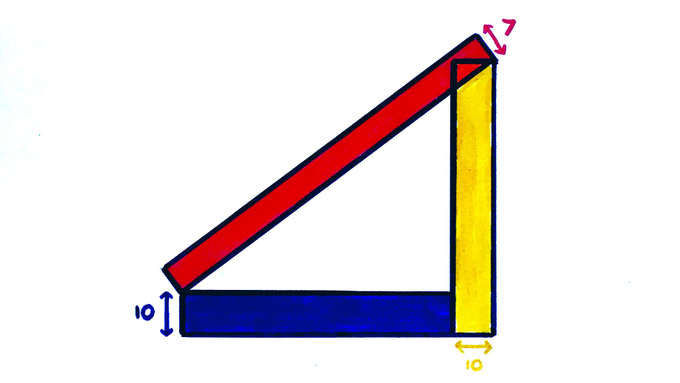
All three of these rectangles have the same area. What is it?
Solution by Pythagoras' Theorem
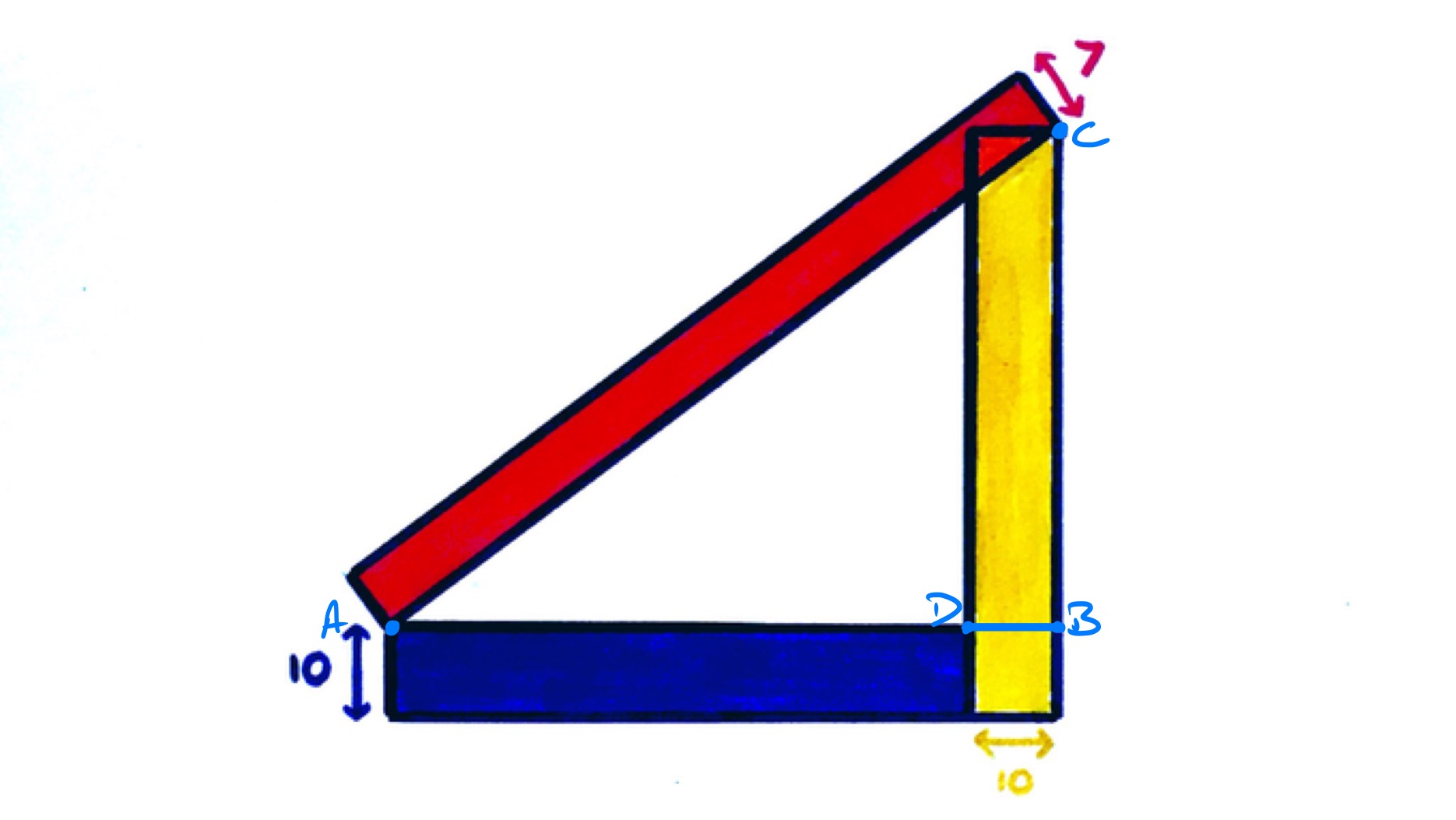
In the above diagram, consider the right-angled triangle . Let be the length of , then has length and has length . Let be the length of . Then applying Pythagoras' theorem to triangle yields:
As the rectangles have the same area, also so . Putting this into the above equation,
which simplifies to , and this simplifies further to and so . The area of the rectangles is therefore .