Notes
three congruent triangles in a semi-circle solution
Solution to the Three Congruent Triangles in a Semi-Circle Puzzle
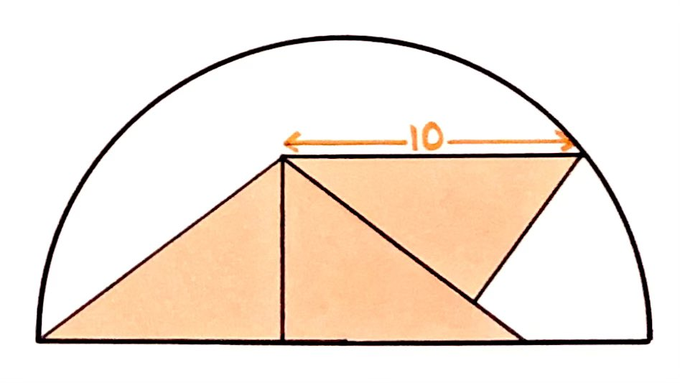
The three triangles are congruent. What’s the area of the semicircle?
Solution by Circle Geometry
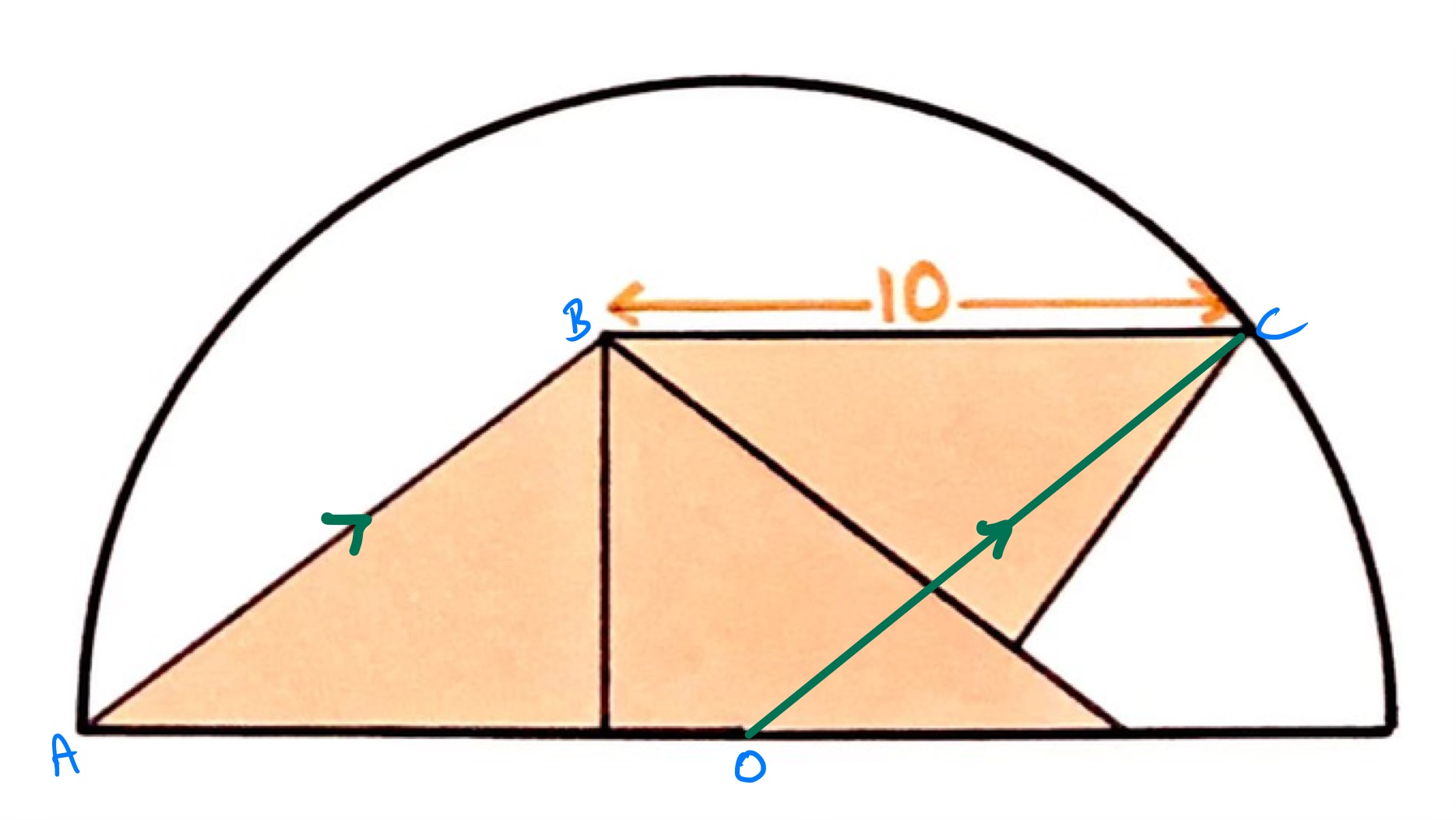
In the diagram above, the point is on the base of the semi-circle so that is parallel to . Since is parallel to , the quadrilateral is a parallelogram. The lengths of and are the same since the triangles are all congruent, so the quadrilateral is actually a rhombus. This means that the lengths of and are equal (and both equal to the length of ). The point is therefore on the diameter and equidistant from two points on the circumference, hence is the centre of the circle. The radius is therefore and the area of the semi-circle is .