Notes
three congruent squares overlapping a square solution
Solution to the Three Congruent Squares Overlapping a Square Puzzle
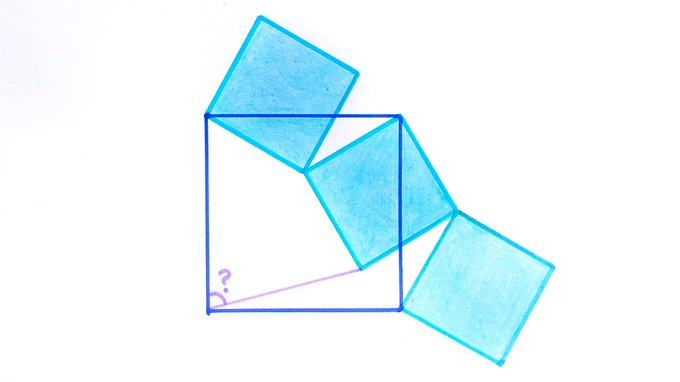
The total area of the three identical squares is equal to the area of the large square. What’s the angle?
Solution by Isosceles Triangles, Angles at a Point, Angles at a Point on a Straight Line, and Area Scale Factor
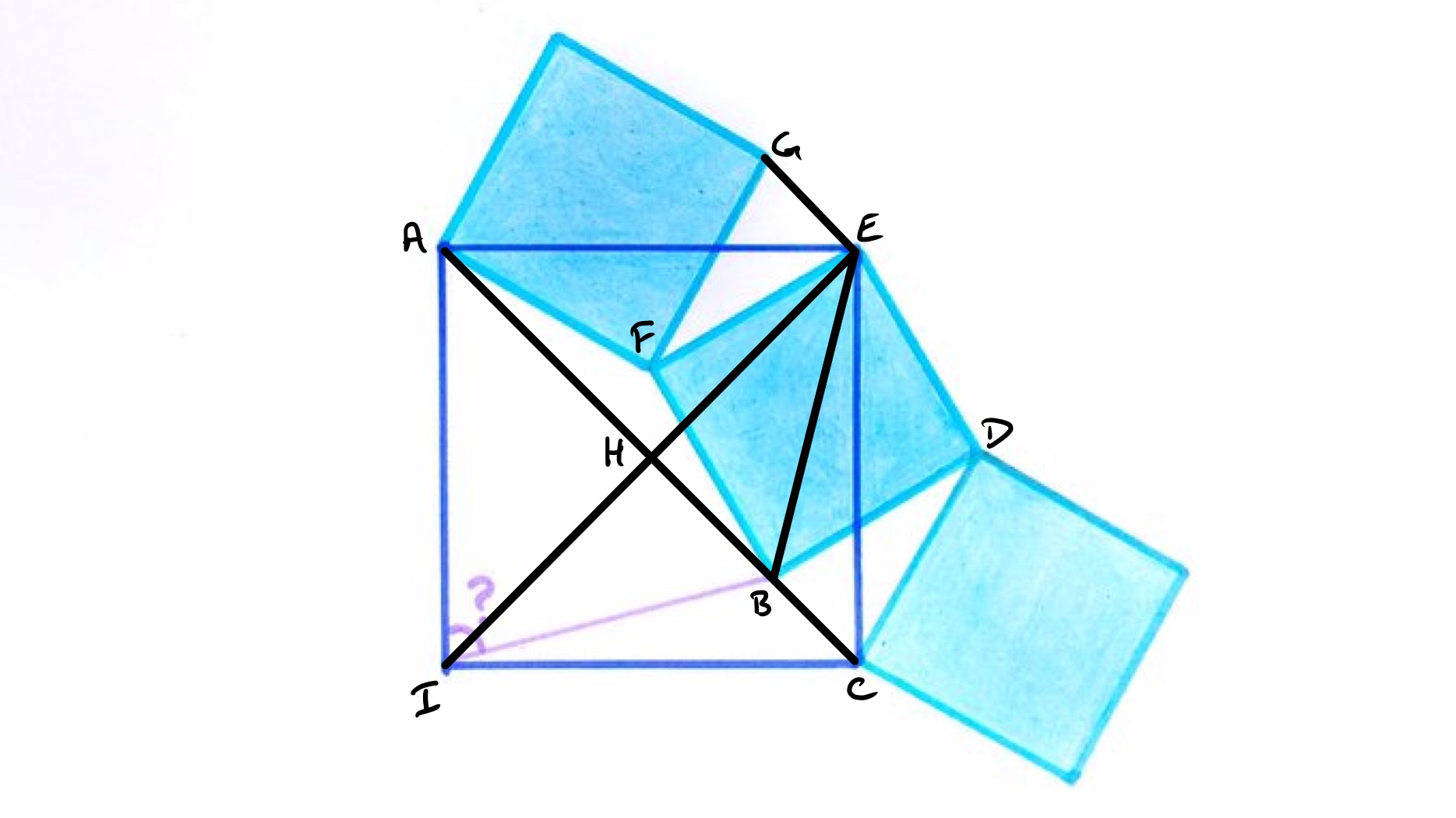
The first step is to establish that point lies on the diagonal .
Consider triangles and . These are congruent as the sides match in length. Therefore angles and are equal, so triangles and are also congruent to each other. By considering the angles at , since angles at a point add up to , angles and add up to . So using angles in isosceles triangles, angles and add up to . Therefore angle is so is a straight line.
As the total area of the three squares is equal to the area of the large square, the length scale factor from the small to the large is . This means that has length times that of . As it is a right-angled triangle, this establishes that is half an equilateral triangle. By symmetry, so is triangle and so angle is . Angle is therefore .