Notes
three congruent rectangles iii solution

Solution to the Three Congruent Rectangles III Puzzle

Solution by Pythagoras' Theorem and Congruency

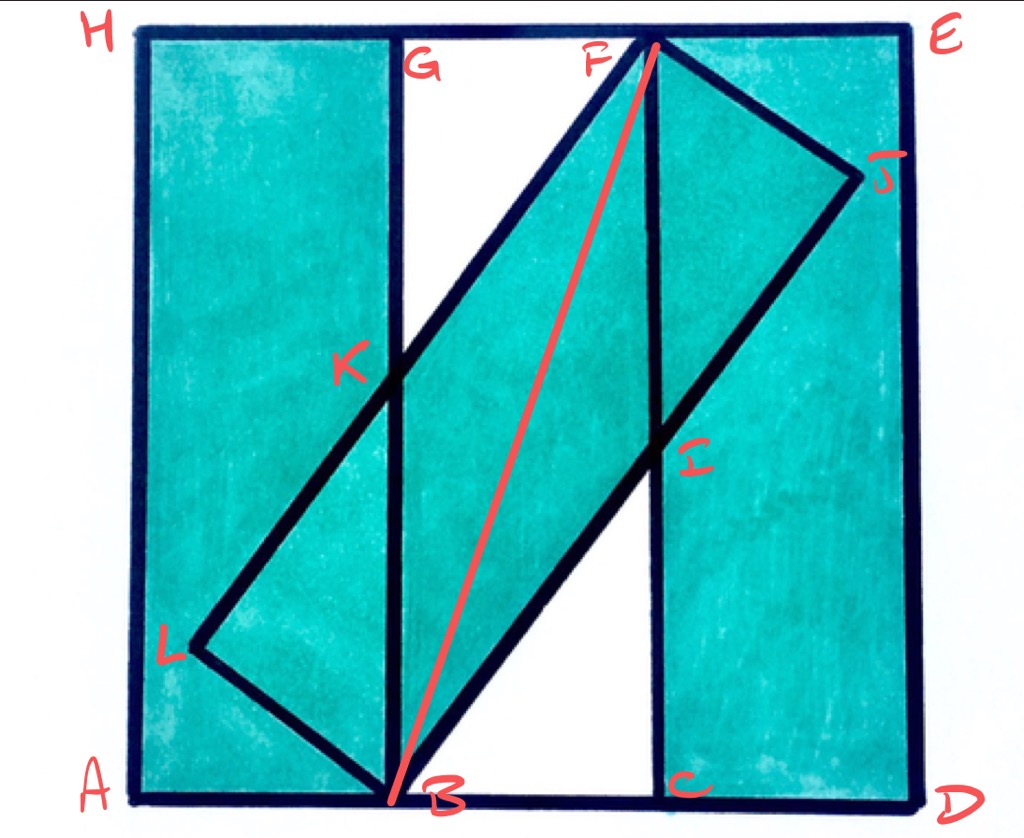
The first step is to establish that the tilted rectangle would fit in the middle of the square. That is, with the points labelled as above then rectangles $B J F L$ and $B C F G$ are congruent.

This is a consequence of Pythagoras' theorem. The green rectangles are all congruent, so $F C$ and $B J$ have the same length. Therefore, triangles $B F C$ and $B F J$ are right-angled triangles that have two sides of the same length, and therefore have all three sides the same.

Triangles $B C I$ and $F J I$ are therefore congruent since both are right-angled, the lengths $B C$ and $F J$ are the same, and the angles $B \hat{I} C$ and $F \hat{I} J$ are equal since they are vertically opposite. Therefore, the lengths of $F I$ and $B I$ are the same.

Each of the three rectangles consists of one third of the outer square, so the ratio of the side lengths of the rectangles is $1 : 3$.

Let $B C$ have length $1$. Then $C F$ has length $3$, so the sum of the lengths of $C I$ and $I B$ is $3$. Let $C I$ have length $x$, then by Pythagoras' Theorem:

Hence $x = \frac{4}{3}$. The area of triangle $B C I$ is therefore $\frac{4}{6}$ and so the white area is $\frac{4}{3}$. The total area of the square is $9$, so the area that is shaded is, as a fraction of the whole: