Notes
three circles solution

Three Circles

Solution by Similar Triangles and Angle Between a Radius and Tangent

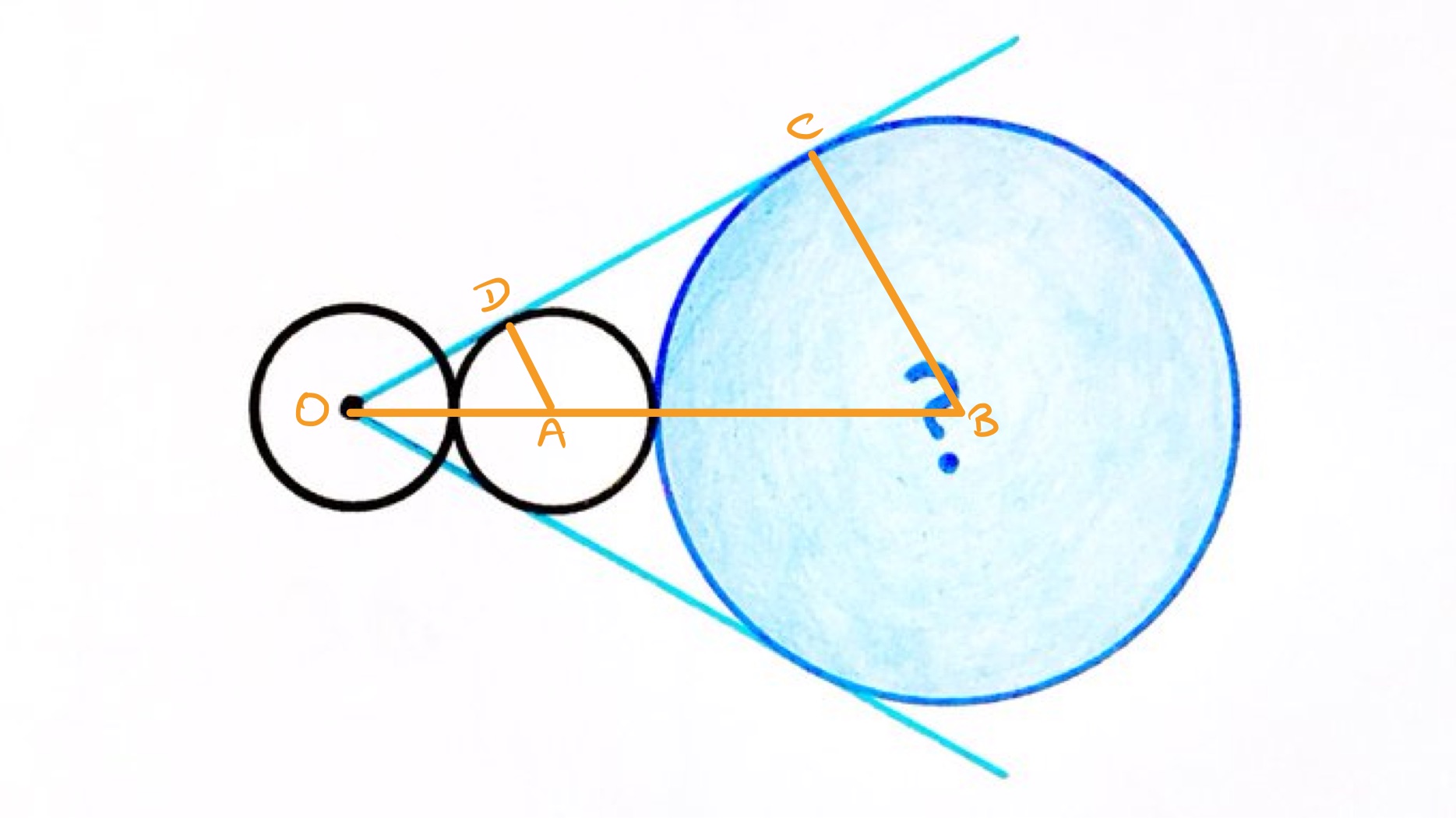
As the two small circles have the same area, they are the same size. Let $r$ be the radius of the small circles and $R$ of the larger one. Then $\pi r^2 = 1$.

With the points labelled as above, angles $O \hat{D} A$ and $O \hat{C} B$ are right-angles as they are the angle between a radius and tangent. So triangles $O D A$ and $O C B$ are similar. In particular, the ratios of the lengths of $A D$ to $O A$ and $B C$ to $O B$ are the same. In terms of the radii of the circles, this means that $R : R + 3 r = 1 : 2$. Equivalently, $R + 3 r = 2 R$ and so $R = 3 r$. The area of the larger circle is then $\pi R^2 = \pi (3 r)^2 = 9 \pi r^2 = 9$.