Notes
three circles in a rectangle solution
Three Circles in a Rectangle
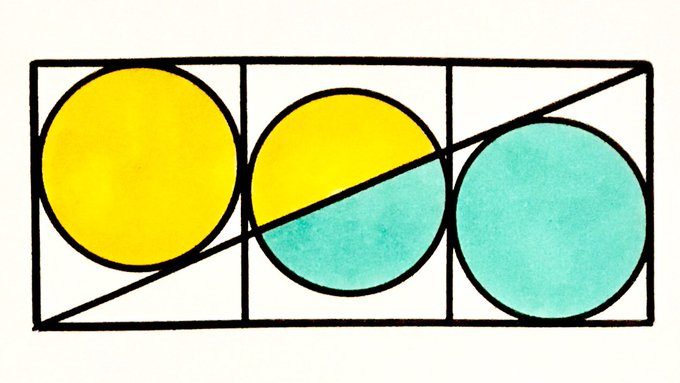
The circles each have radius . What’s the area of the rectangle?
Solution by Similar Triangles
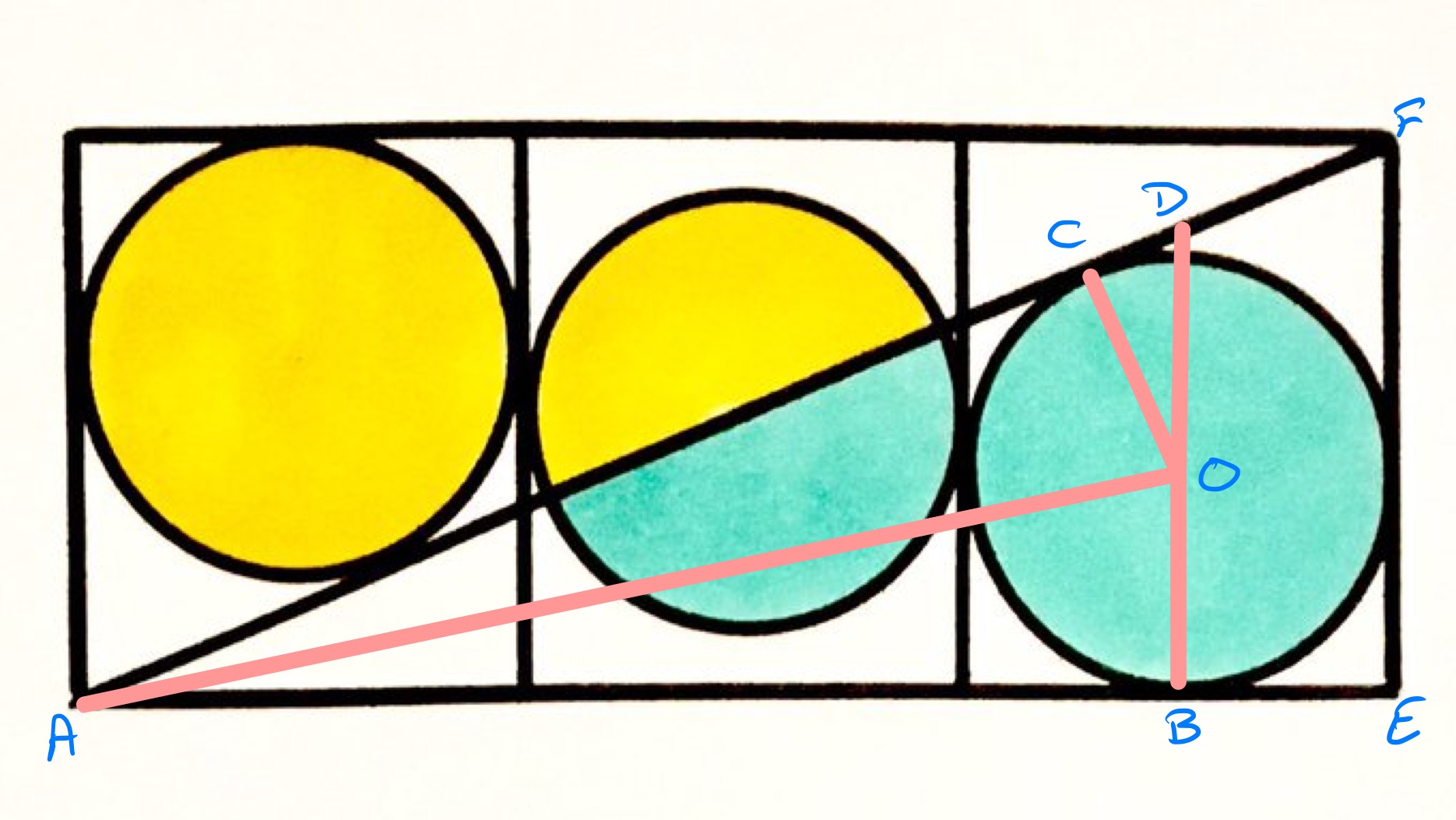
With the points labelled as above, triangles and are congruent and so is the same length as , which is . Triangles and are both right-angled and share the angle at , so are similar.
Let be the length of and of . The lengths of are, from shortest to longest, , , and of are , , . So and . Solving this gives and . This means that has length .
Triangle is also similar to . The length of is , so the length of is ths of the length of , so is . The area of the rectangle is the .