Notes
three circles in a rectangle ii solution
Solution to the Three Circles in a Rectangle II Puzzle
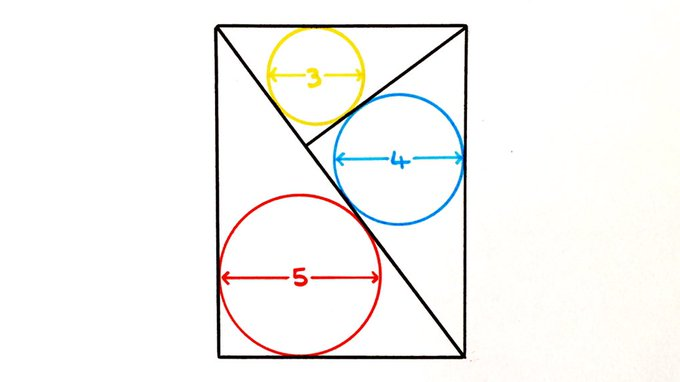
I’ve stacked three right-angled triangles to make this rectangle. What’s its area?
Solution by Similar Triangles
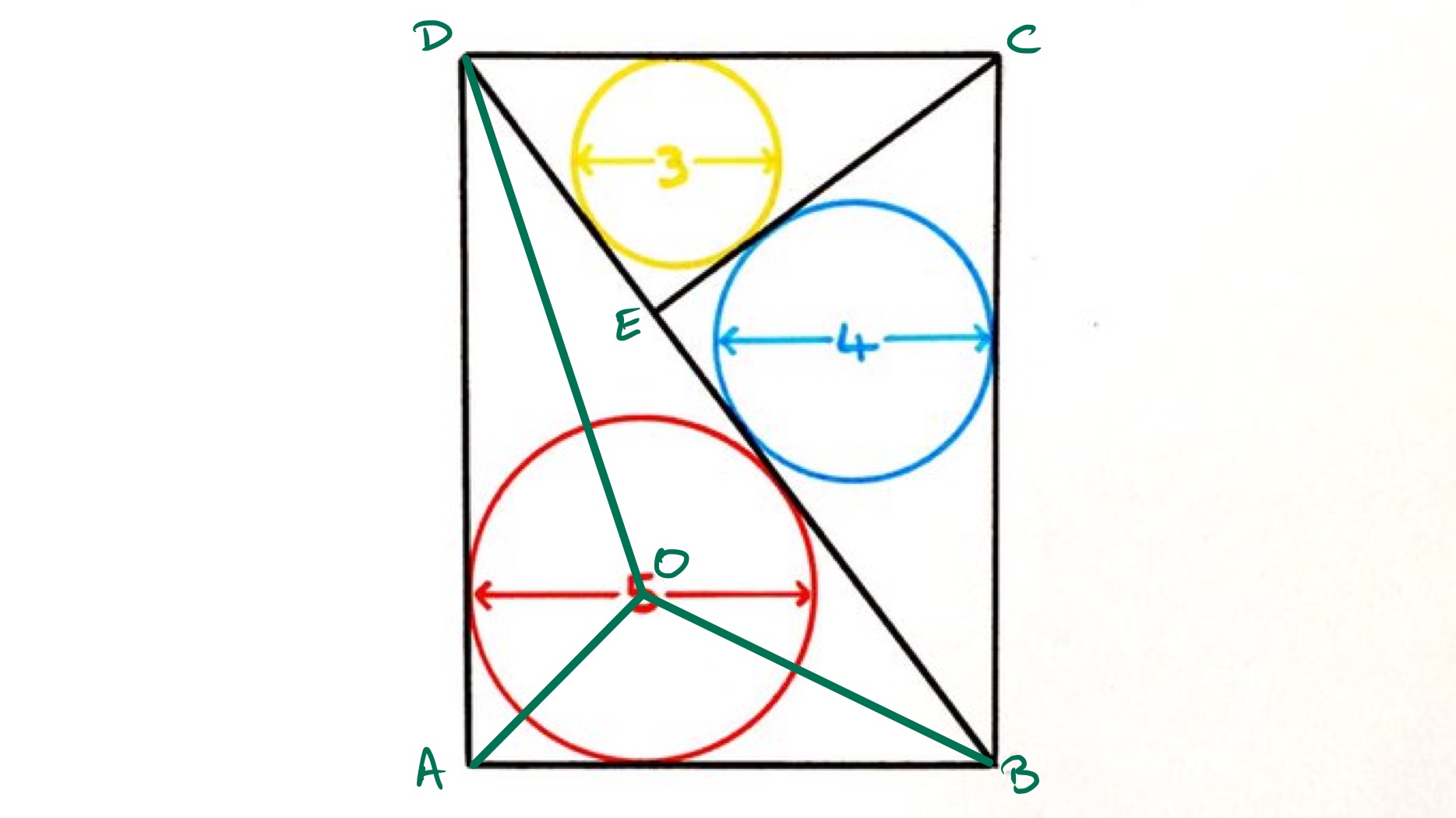
All three triangles are right-angled triangles, angles and add up to , and angles and also add up to , so all three triangles are similar. The length scale factors from the largest to the other two are and . Let be the length of the diagonal, , so then has length and has length .
To compute , consider the area of the largest triangle. Using the formula for the area of a triangle, it is . Using the centre of the circle, the triangle can be decomposed into three triangles each with height the radius of the in-circle and bases the sides of the original triangle. The area calculated this way is . Equating these gives .
The sides of the rectangle are then and so its area is .