Notes
three circles and two semi-circles in a circle solution
Solution to the Three Circles and Two Semi-Circles in a Circle Puzzle
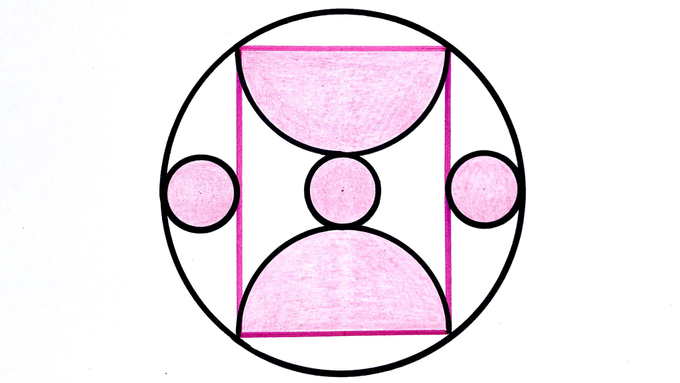
The three small circles are the same size. What fraction of the large circle is shaded?
Solution by Pythagoras' Theorem
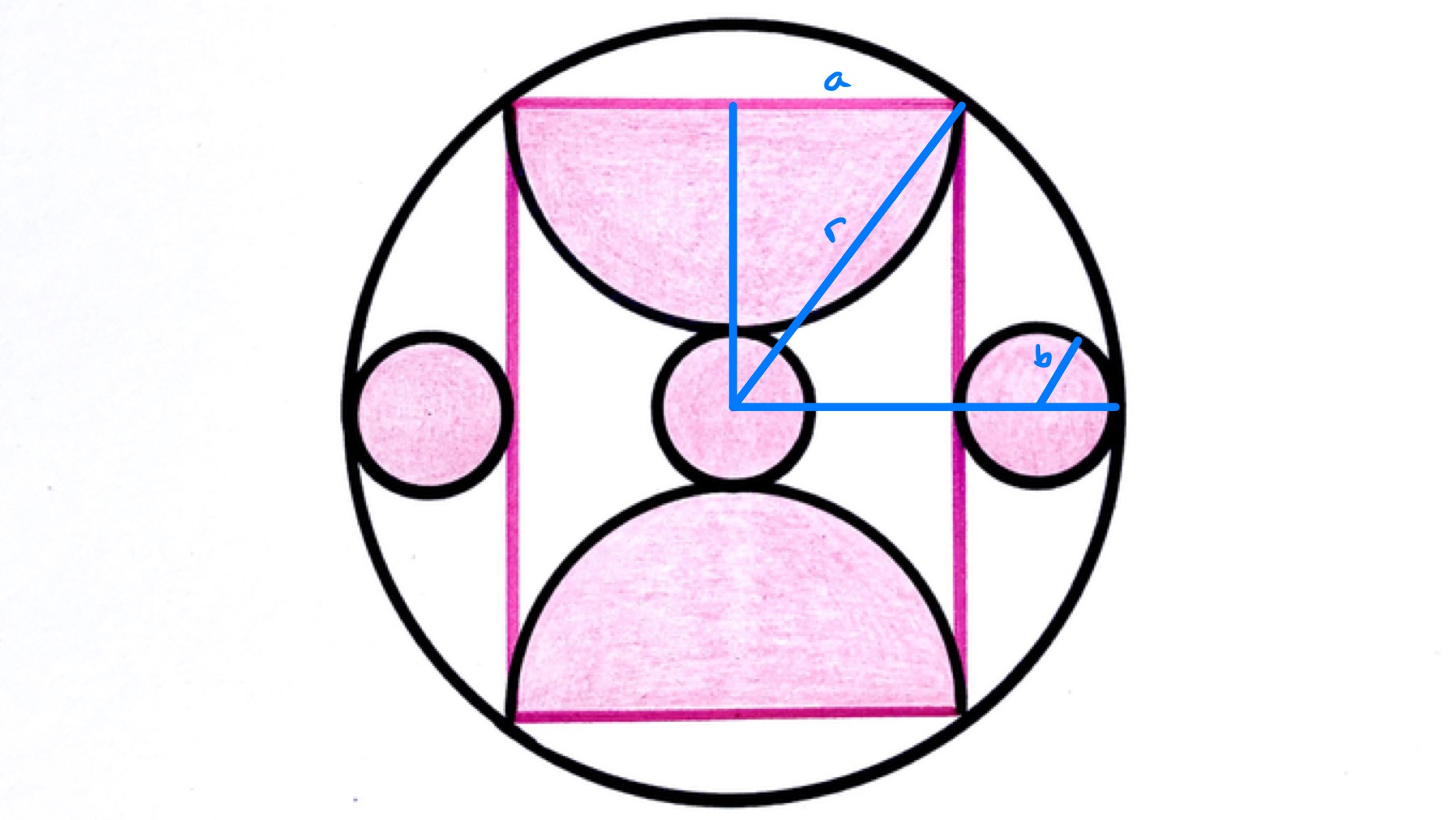
As in the above diagram, let be the radius of the smallest circle, of the middle, and of the outer. Then by considering the horizontal radius, . Applying Pythagoras' Theorem to the blue triangle yields . Putting these together gives:
So either or . As and are lengths, neither can be negative and so it must be the case that . Then .
The area of the large circle is and the shaded area is . So the area of the large circle is and of the shaded area is . The fraction that is shaded is therefore .