Notes
three aligned squares solution
Three Aligned Squares
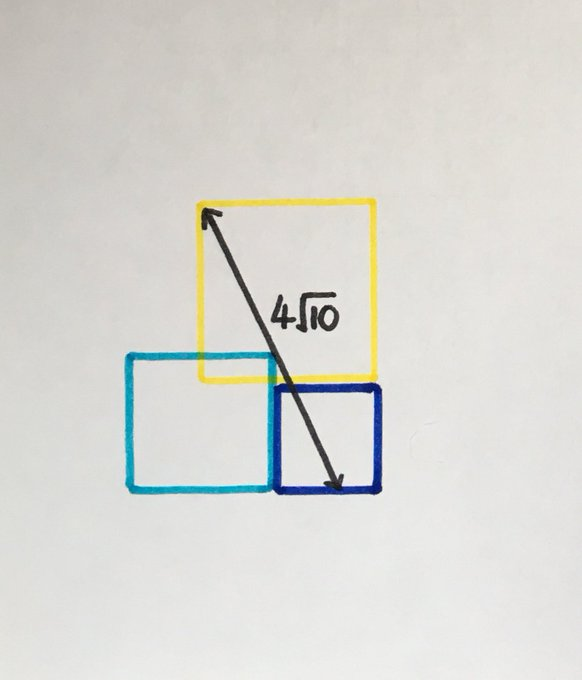
The sides lengths of the three squares are consecutive integers. What’s the total area?
Solution by Pythagoras' Theorem
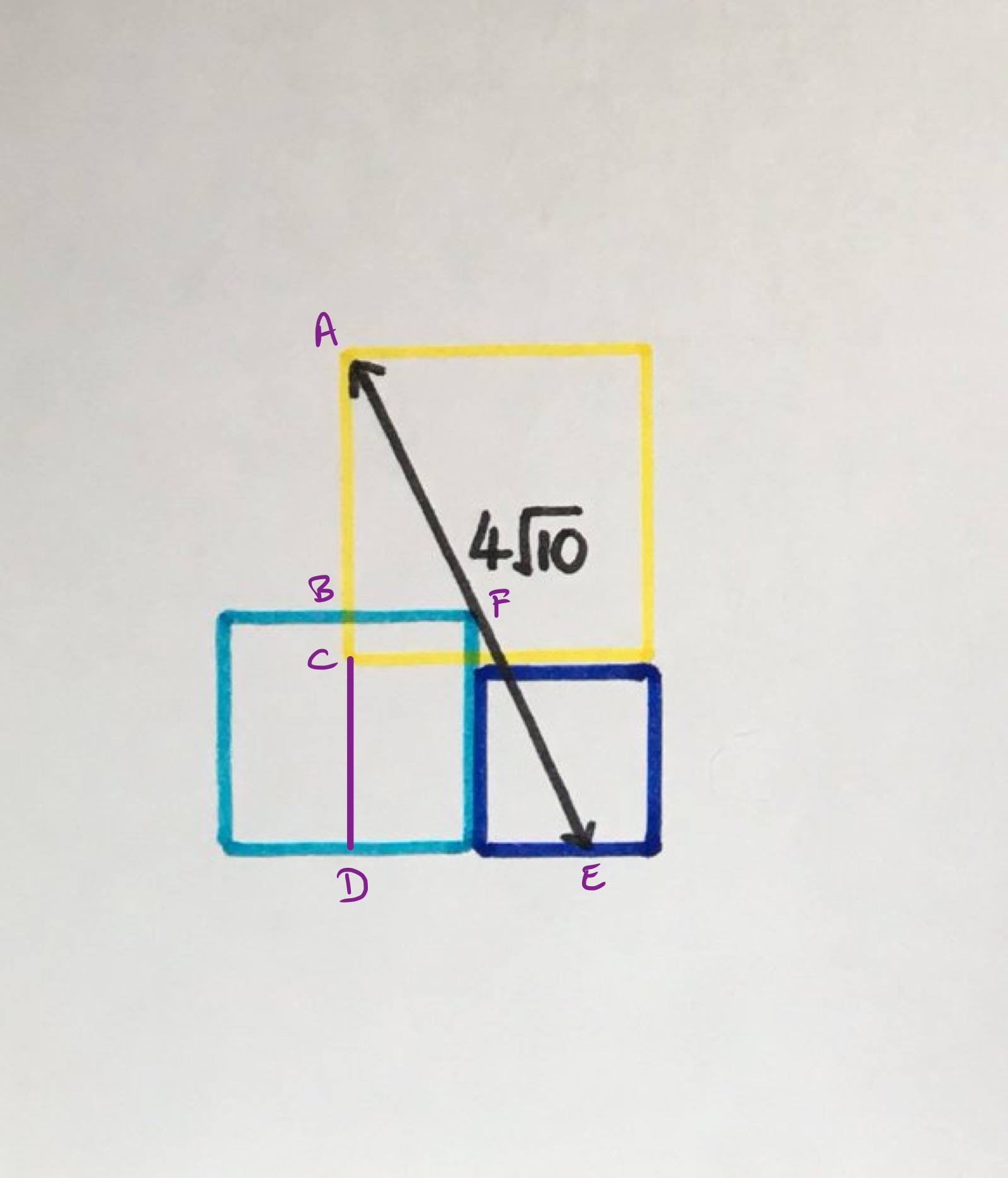
As the lengths of the sides of the three squares are consecutive integers, they can be written as , , and where is the length of the side of the light blue square.
Since has length , the length of is , so is the midpoint of . The length of is . Since is the midpoint of , is the midpoint of and so has length . Applying Pythagoras' theorem to triangle shows that which means that . The squares therefore have sides , , and .
Since has length and has length , the total area of the shape is .