Notes
three adjacent triangles solution
Solution to the Three Adjacent Triangles Puzzle
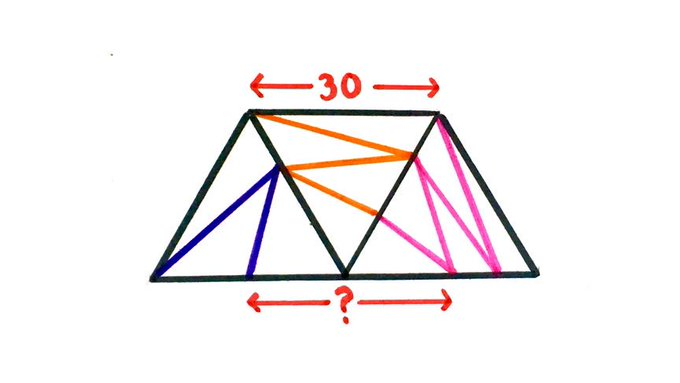
Each equilateral triangle has been divided into pieces of equal area. What’s the missing length?
Solution by Area of a Triangle
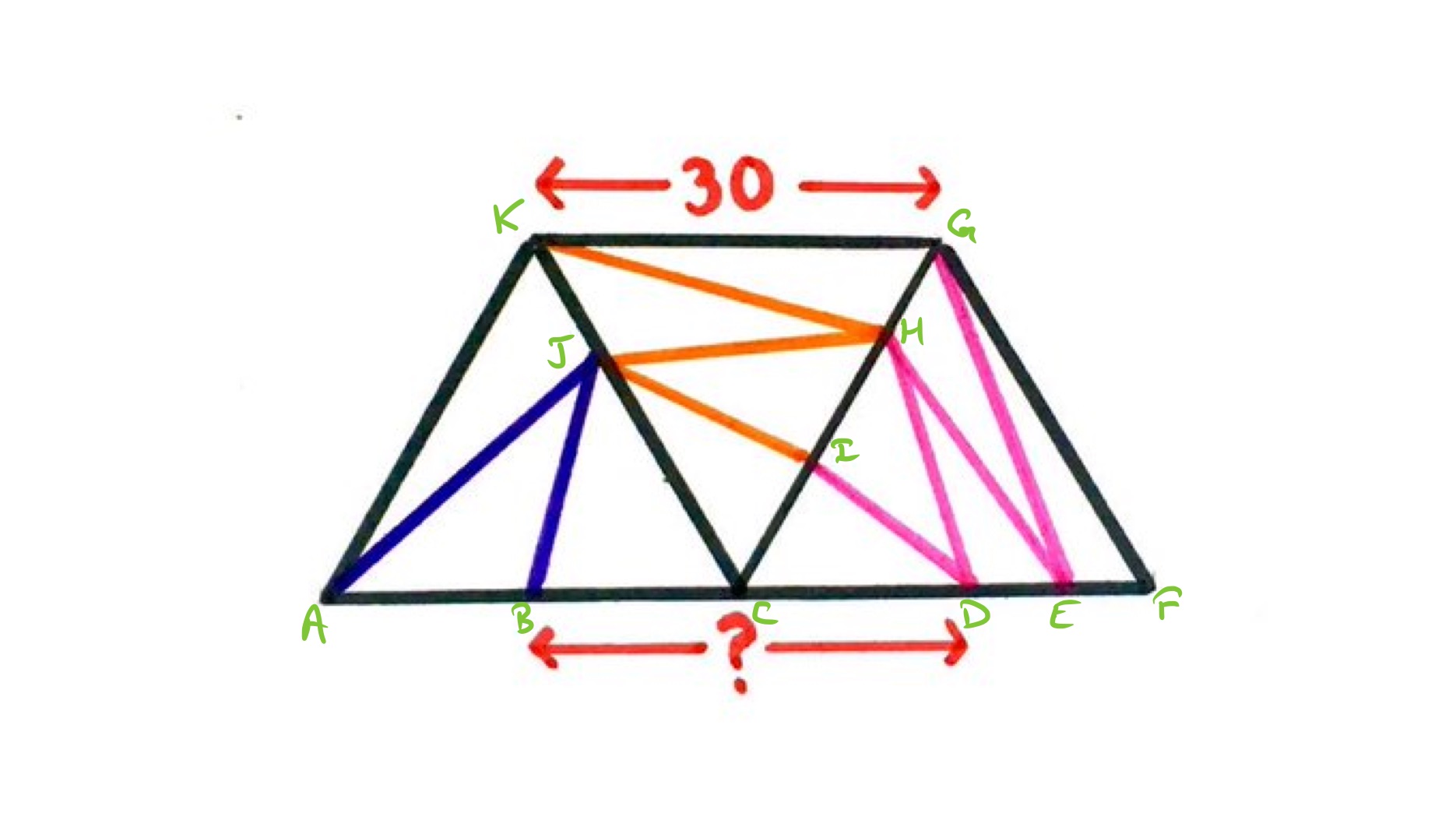
Consider the diagram with the points labelled as above. Starting on the left, triangles and have the same area and the same height above the line , so the lengths of and must be the same. As has length , therefore has length .
On the right, triangle has the same height as the full triangle but a fifth of the area, so must be one fifth of , which is , meaning that is the remaining . Similarly, triangle is one third of triangle so is one third of , which is , meaning that is the remaining .
Putting these together, has length .