Notes
three circles forming a triangle solution

Three Circles Forming a Triangle

Solution by Pythagoras' Theorem

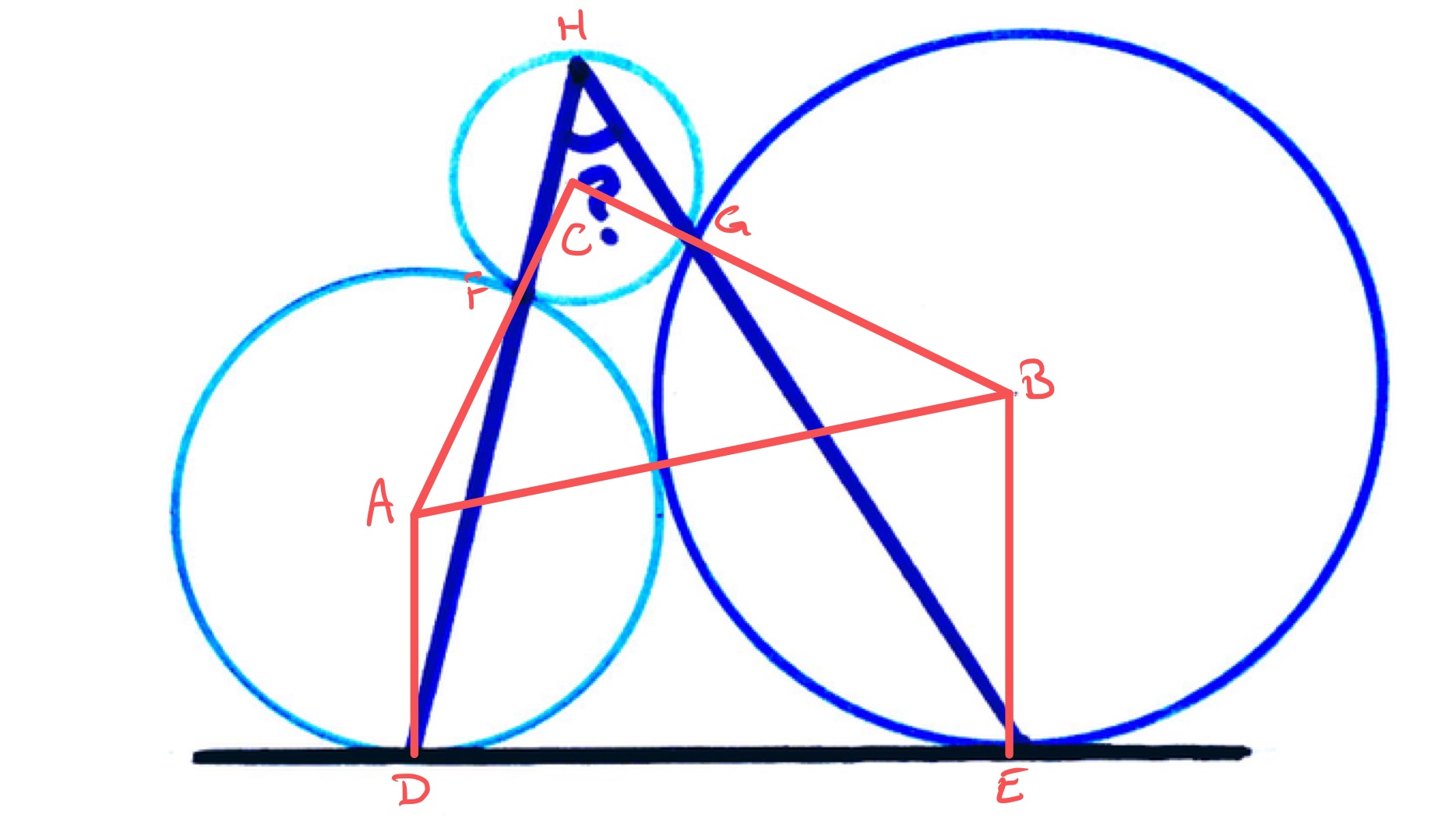
In the above diagram, the points labelled $A$, $B$, and $C$ are the centres of their respective circles. As the circles have diameters $1$, $2$, and $3$, the lengths of the segments $A C$, $B C$, and $A B$ are, respectively, $\frac{1}{2} + 1 = \frac{3}{2}$, $\frac{1}{2} + \frac{3}{2} = 2$, and $1 + \frac{3}{2} = \frac{5}{2}$. These lengths satisfy:

They therefore fit into the identity for the converse to Pythagoras' theorem and so triangle $A C B$ is a right-angled triangle with the right-angle at point $C$. Then since the angle at the centre is twice the angle at the circumference, angle $F \hat{H} G$ is half of $90^\circ$, which is $45^\circ$.