Notes
swirling semi-circles solution
Solution to the Swirling Semi-Circles Puzzle
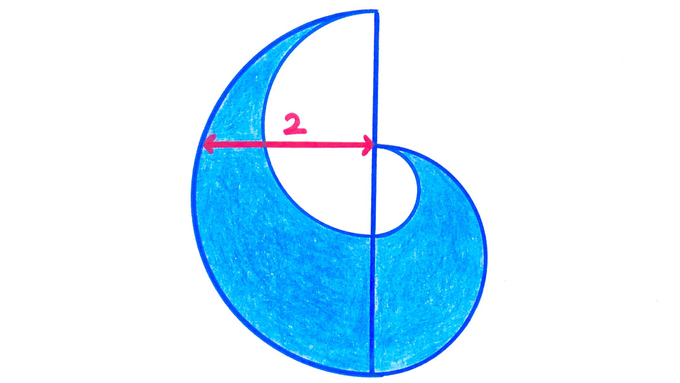
The largest and smallest semicircles are concentric. What’s the shaded area?
Solution by Circle Area and Pythagoras' Theorem
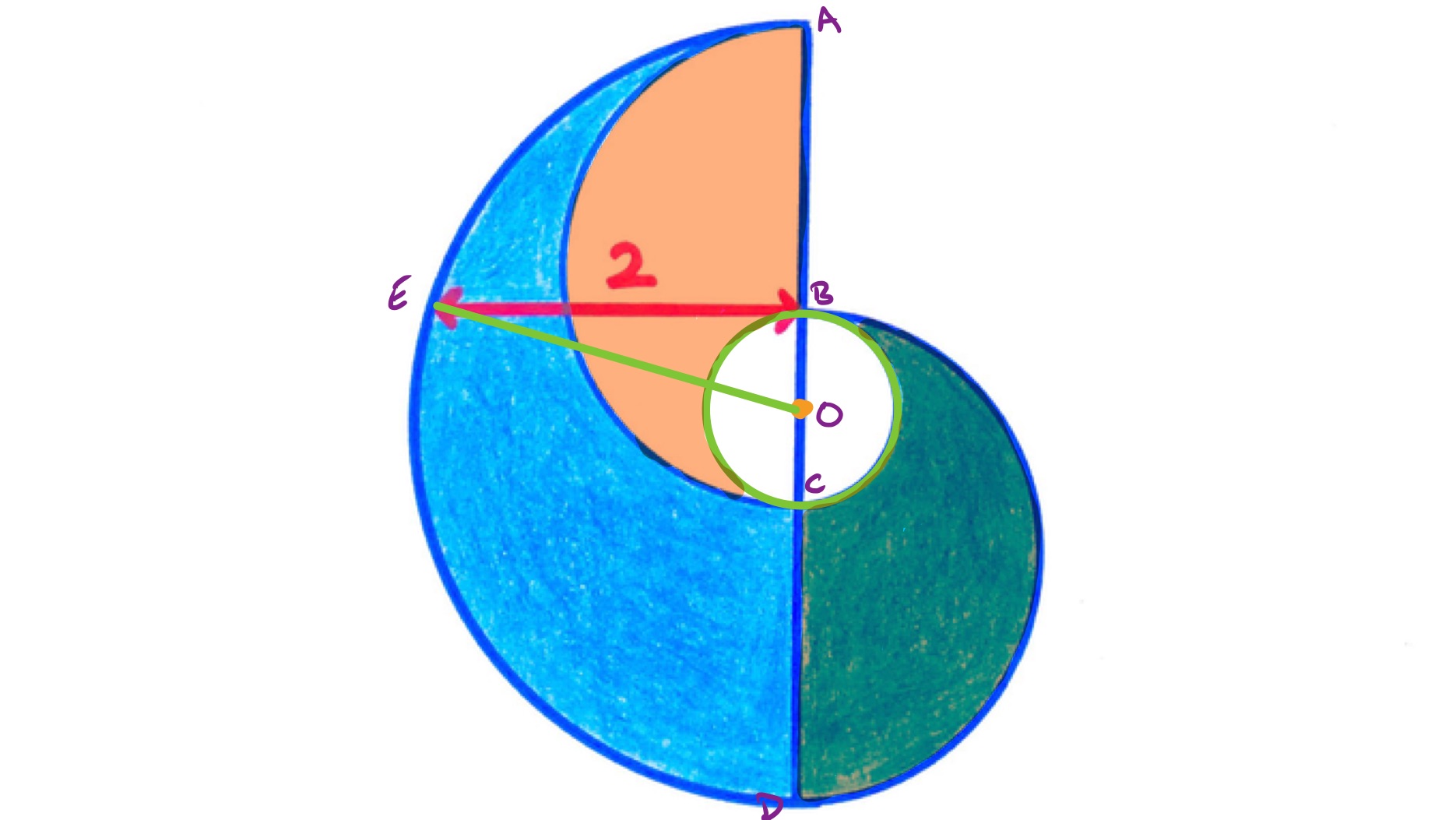
In the above diagram, is the centre of the smallest circle. As the largest and smallest semi-circles are concentric, the lengths of and are equal, so the lengths of and are also equal. These are the diameters of the two middle size semi-circles, so they are the same size. This means that the orange and green areas in the above diagram are congruent.
The shaded area is therefore the same as the difference between the areas of the largest and smallest semi-circles. Let be the radius of the smallest semi-circle and of the largest. These two radii form two sides of the right-angled triangle . So by Pythagoras' theorem,
The area of the shaded region is therefore given by .