Notes
subdivided square solution

Solution to the Subdivided Square Puzzle

Solution by Dissection, Congruence, Similarity, and Area of a Triangle

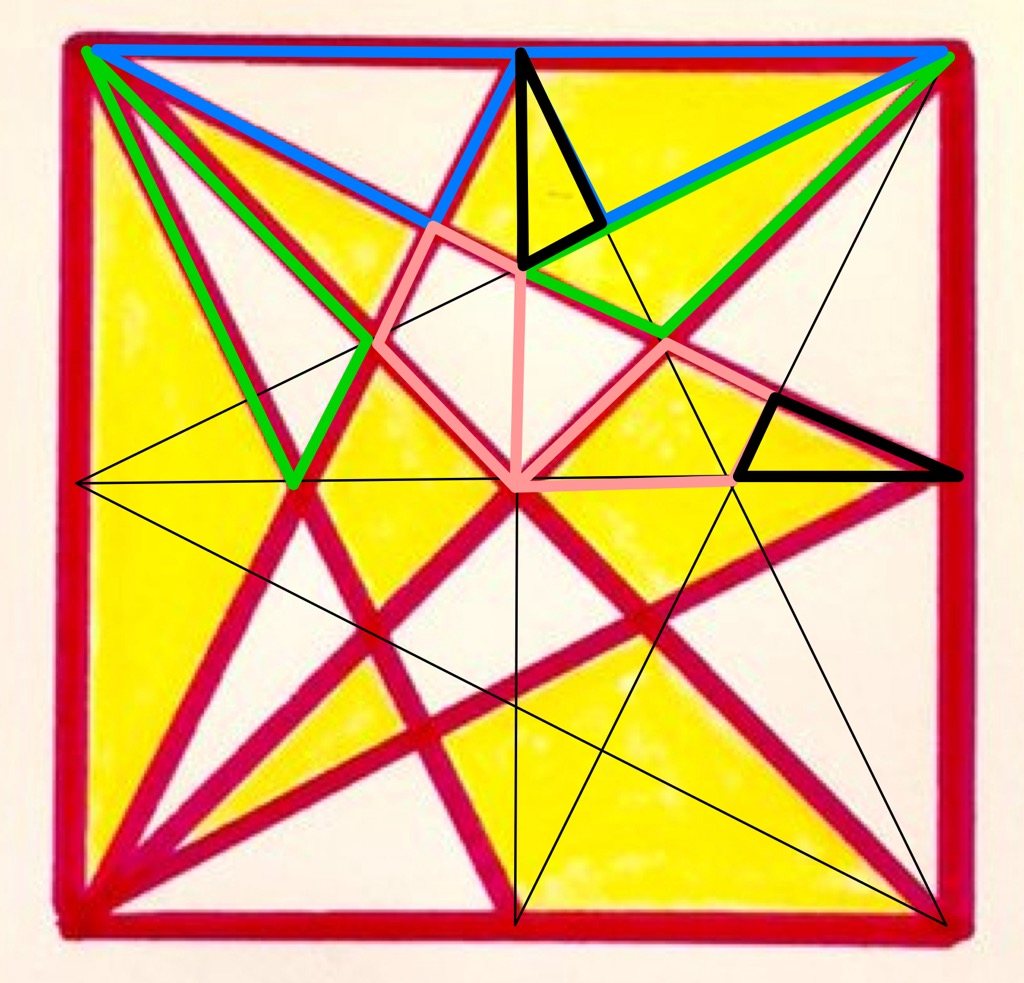
In the above diagram, more lines have been added to divide up the regions. Various regions have been outlined in colour, and the regions with the same colour are congruent. In particular, the blue triangles are congruent; the green triangles are congruent, and the pink kites are congruent. This means that the shaded blue, green, and pink regions can be taken from the right-hand side of the diagram to fill in the unshaded regions in the left. The same can be done with the analogous shapes in the lower half of the diagram. This results in the left-hand side being completely shaded, while the right-hand side is unshaded except for the black triangles, and corresponding triangles in the lower half of the diagram.

The combined blue and black triangle in the upper right corner has total area one sixteenth of the square. This is because its “base” along the top edge is one half of the side of the square, while its “height” is one quarter.

The blue and black triangles are similar, and their length scale factor is the same as the ratio of the sides in the black triangle, which is $1 : 2$, so the blue triangle has area $4$ times that of the black, meaning that the black triangle has area one fifth of the combined blue and black triangle. One black triangle therefore has area $\frac{1}{80}$th of the whole square.

Since there are four such triangles, the fraction of the square that is yellow is: