Notes
subdivided parallelogram solution
Solution to the Subdivided Parallelogram Puzzle
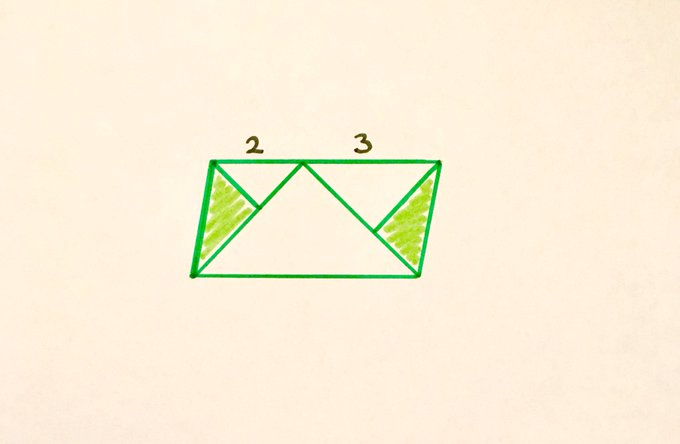
Unshaded triangles are isosceles. What fraction of the parallelogram is shaded?
Solution by Similar Triangles and Angles in Parallel Lines
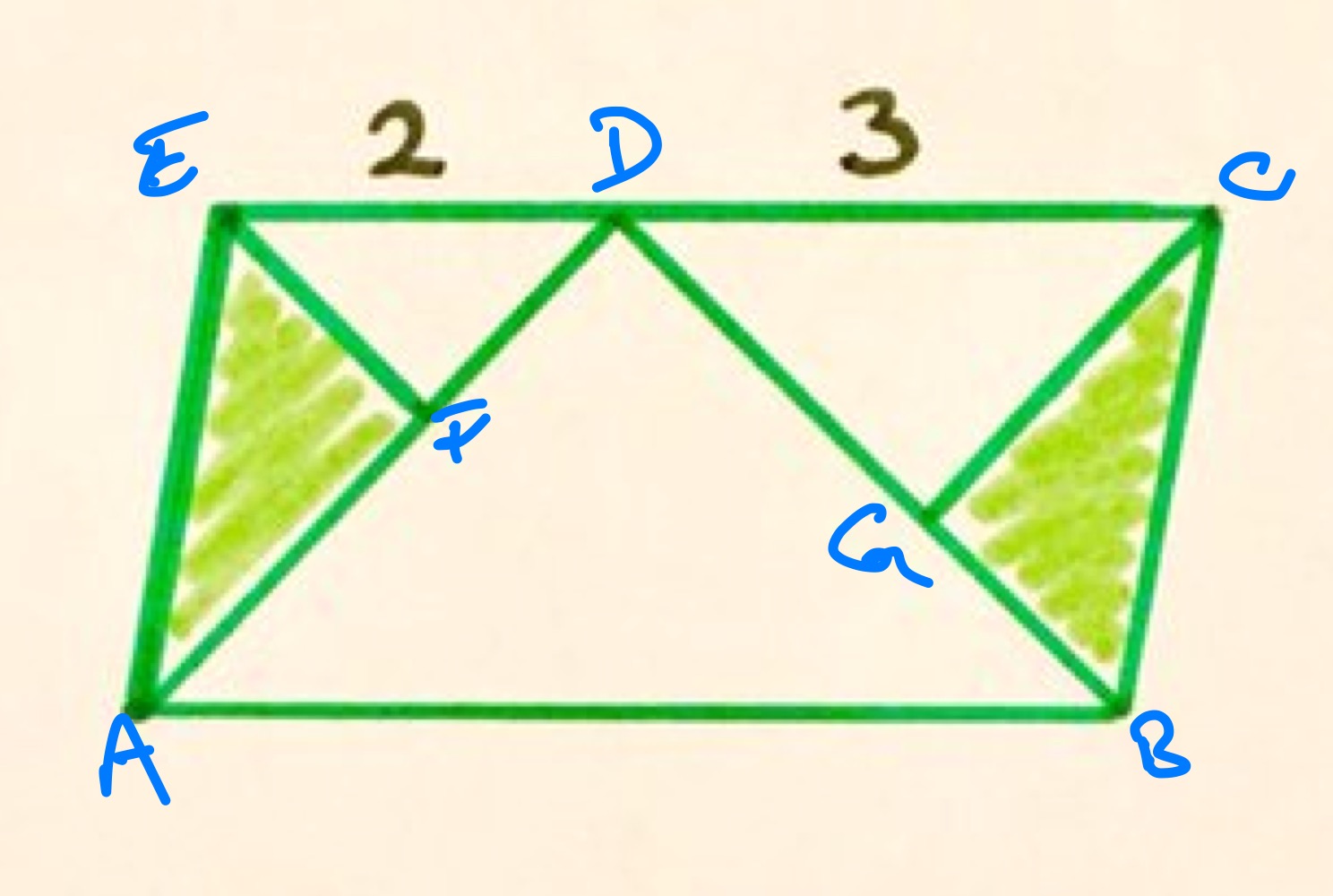
Note: there is a hidden assumption here that the bases of the unshaded triangles lie along the edges of the outer parallelogram.
Consider the diagram as labelled above. As the outer shape is a parallelogram, line segments and are parallel. Therefore by angles in parallel lines, angles and are equal, as are angles and .
The base angles of the isosceles triangles , , and are therefore all the same and so these triangles are all similar. The sides , , and correspond, so the scale factors from the larger triangle to each of the smaller are, respectively, and . The corresponding area scale factors are and .
The area of triangle is half that of the parallelogram so the unshaded area is
of the parallelogram. The shaded area is therefore ths of the parallelogram.