Notes
subdivided hexagon solution
Solution to the Subdivided Hexagon Puzzle
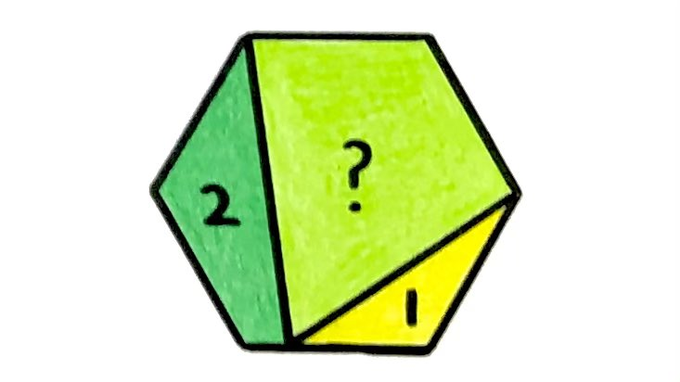
What’s the missing area in this regular hexagon?
Solutions using Triangle Areas
Solution One
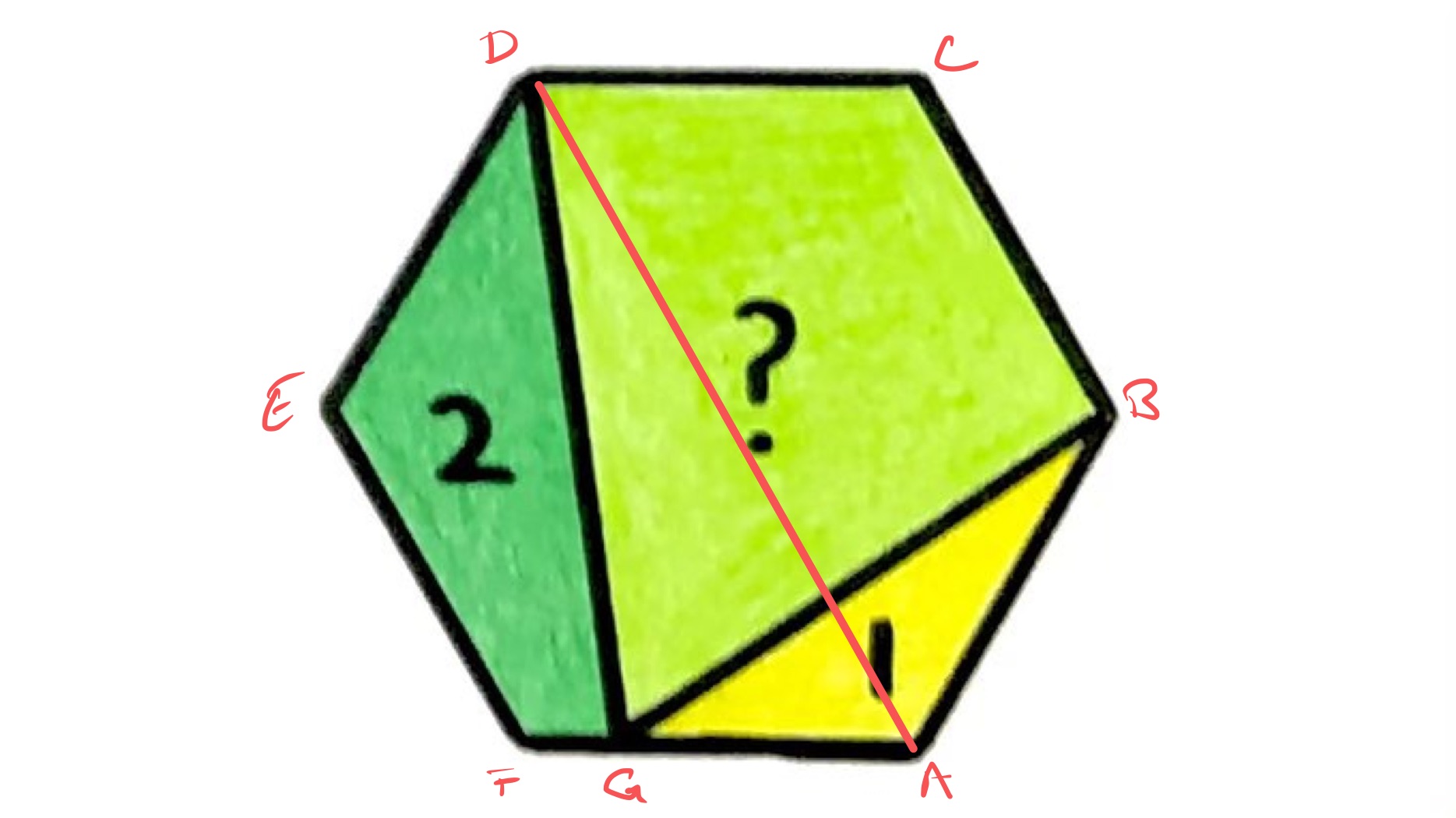
In the above diagram, triangles and have the same base, , and the height of point above this base is half of that of . So triangle has area twice that of , namely .
The regions and together make up half of the hexagon and, by the above, have combined area . The area of the hexagon is therefore .
Solution Two
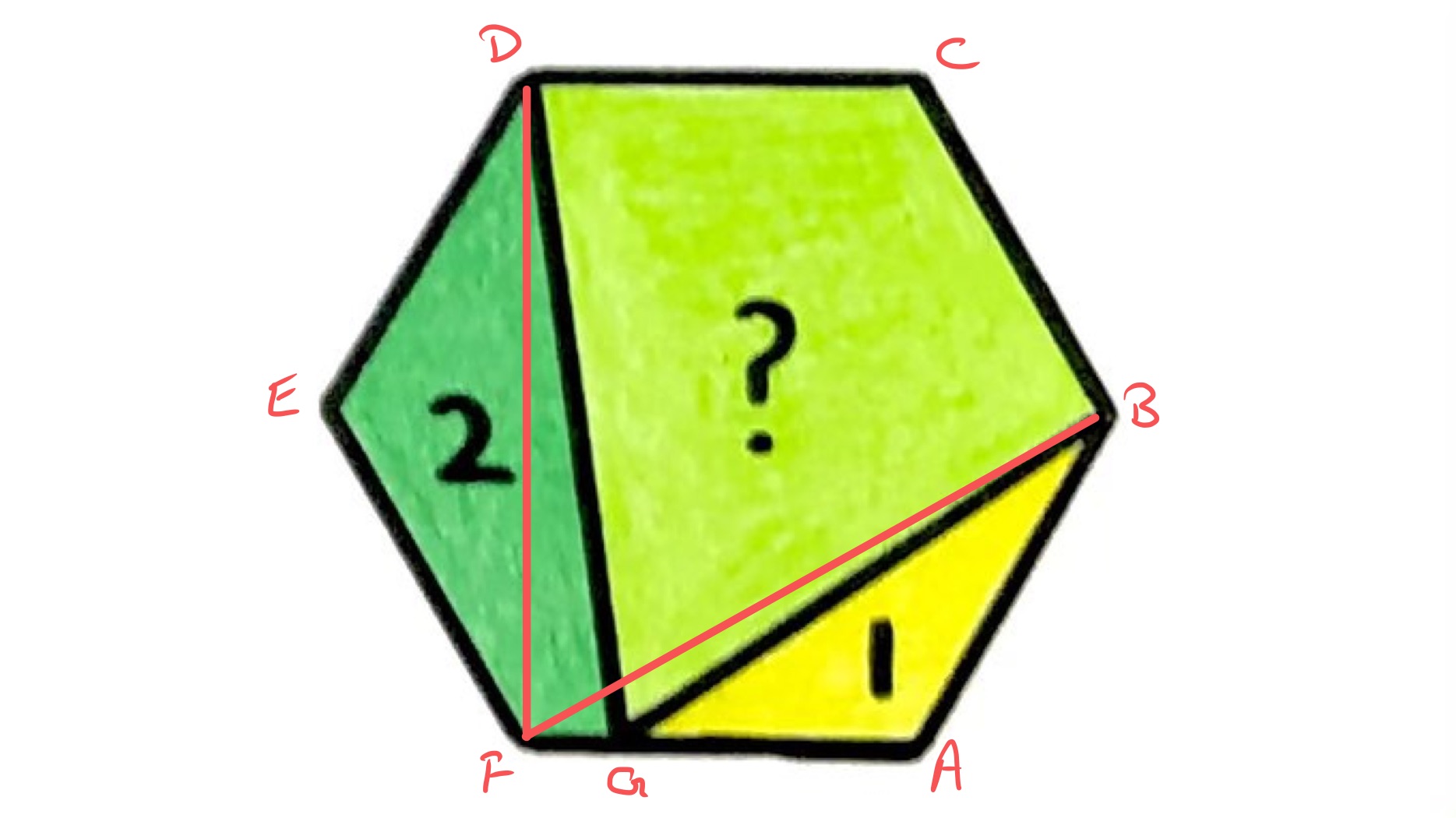
Let be the area of triangle . As triangles and have the same base, , and the height of point above this base is half of that of , the area of is twice of that of , so is .
The regions and are congruent so have the same area. The area of is and of is , so . Solving this gives and so the area of is .
The area of the hexagon is six times that of , so is .