Notes
striped dodecagon solution
Solution to the Striped Dodecagon Puzzle
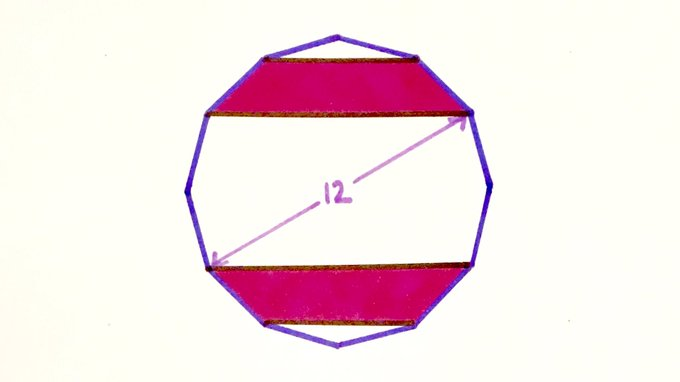
This dodecagon is regular. What’s the total shaded area?
Solution by Triangle Area
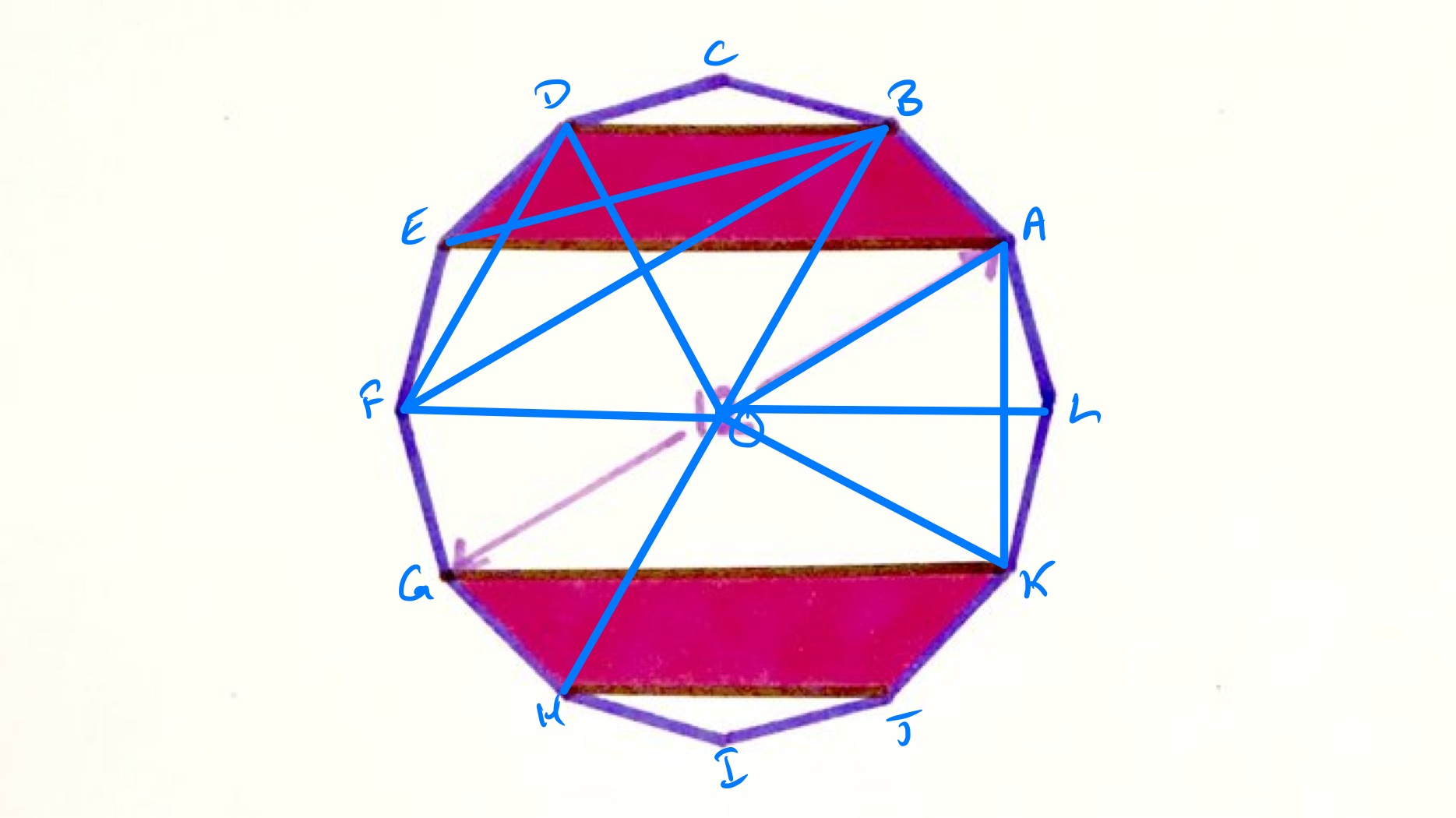
With the points labelled as above, consider the upper shaded region. This can be decomposed into two triangles, and . Triangle is congruent to triangle , so the shaded region has the same area as the quadrilateral . This region can be decomposed into triangles and . As the line segments and are parallel, sliding the apex of triangle from along to does not change its area - the “height” of the apex above remains constant. So triangles and have the same area. Thus the shaded region has the same area as the kite . This in turn is one sixth of the area of the full dodecagon, so when combined with the lower shaded region then the shaded region is one third of the full dodecagon.
To find the area of the dodecagon, consider the triangles and . The first of these, , is equilateral and so has length . Then since the line segment cuts perpendicularly, triangle has base of length and height half of of length , so has area . This is one twelfth of the area of the whole polygon, which therefore has area .
The shaded region then has area .