Notes
stacked triangles solution
Solution to the Stacked Triangles Puzzle
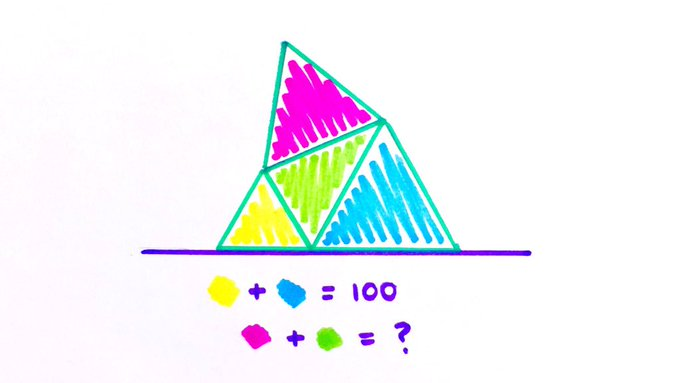
Three of the triangles in this stack are equilateral. Find the sum of the pink and green areas.
Solution by Pythagoras' Theorem and Equilateral Triangles
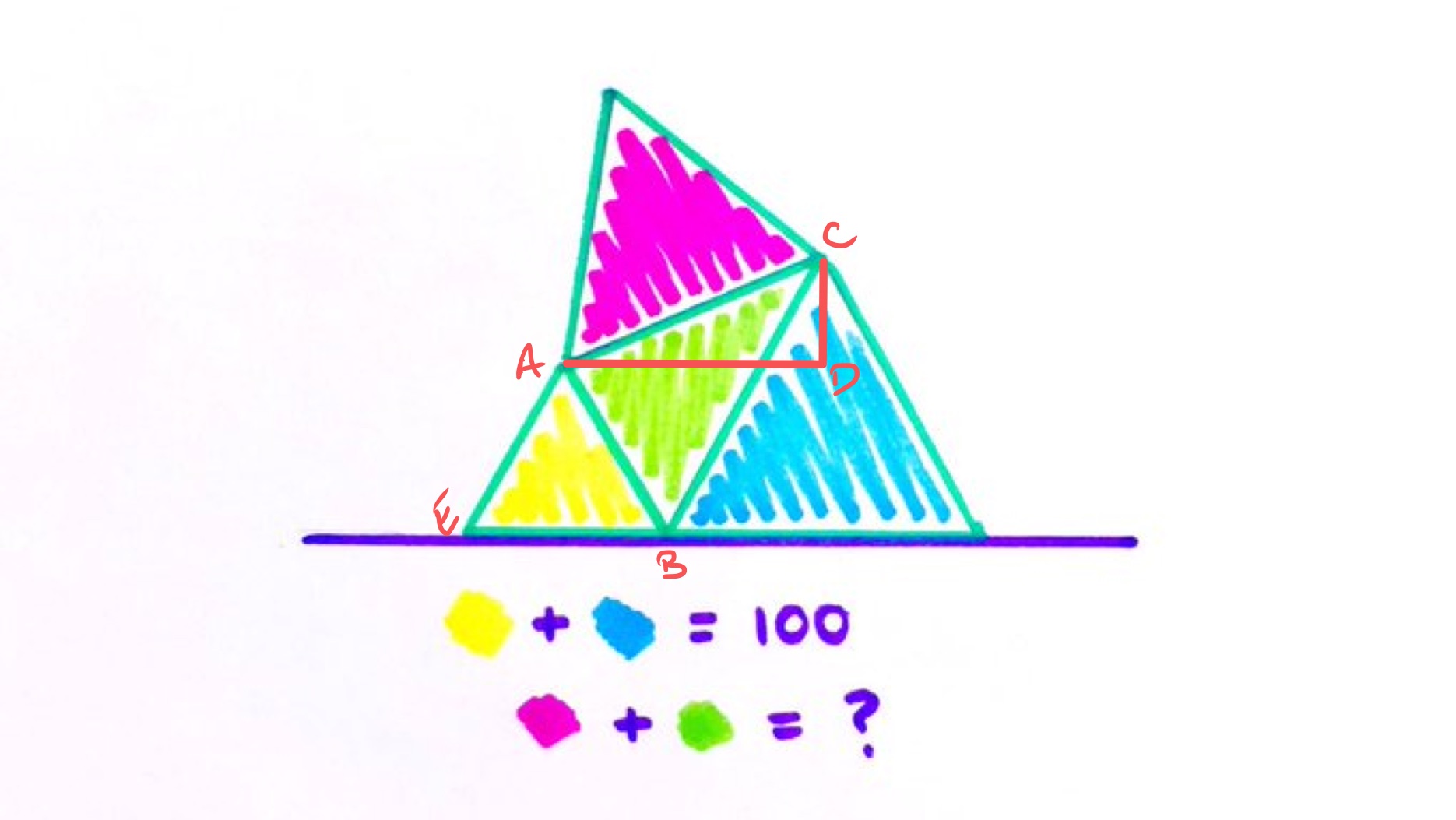
With the points labelled as above, let be the length of , of , and of . Then these are also the lengths of the blue, purple, and yellow triangles respectively. The area of an equilateral triangle is times the square of its side length, so considering the areas of the blue and yellow triangles gives:
Line segments and are parallel so the “height” of above is the same as the “height” of above , which is . The green area is therefore
Considering the right-angled triangle , the length of is and the length of is . Pythagoras' theorem therefore gives the following formula for :
The area of the purple triangle is so the combined purple and green regions have total area:
Solution by Cosine Rule and Area of a Triangle
With , , and as above, the cosine rule applied to the green triangle gives:
So .
The sine rule for the area of a triangle shows that the areas of the three triangles are:
So the purple and green areas are
Solution by Invariance Principle
If the yellow and blue triangles are the same size, the green triangle becomes equilateral and all four are in fact congruent, whereupon the area of the green and purple is the same as that of the yellow and blue.