Notes
stacked squares inside two squares solution

Solution to the Stacked Squares Inside Two Squares Puzzle

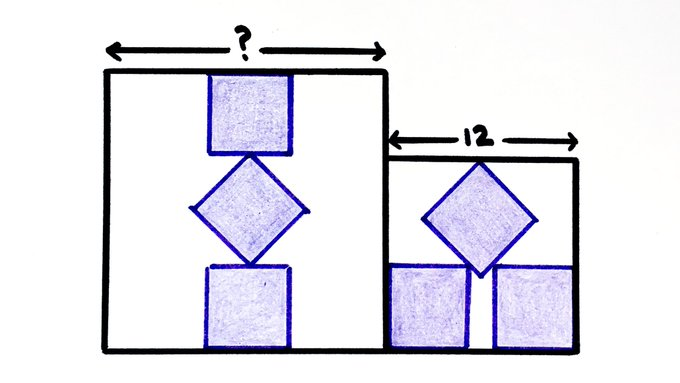
Stacked Squares Inside Two Squares

The purple squares are all the same size. I’ve arranged three of them symmetrically inside each of the two black squares. What’s the missing length?

Solution by Lengths in Squares

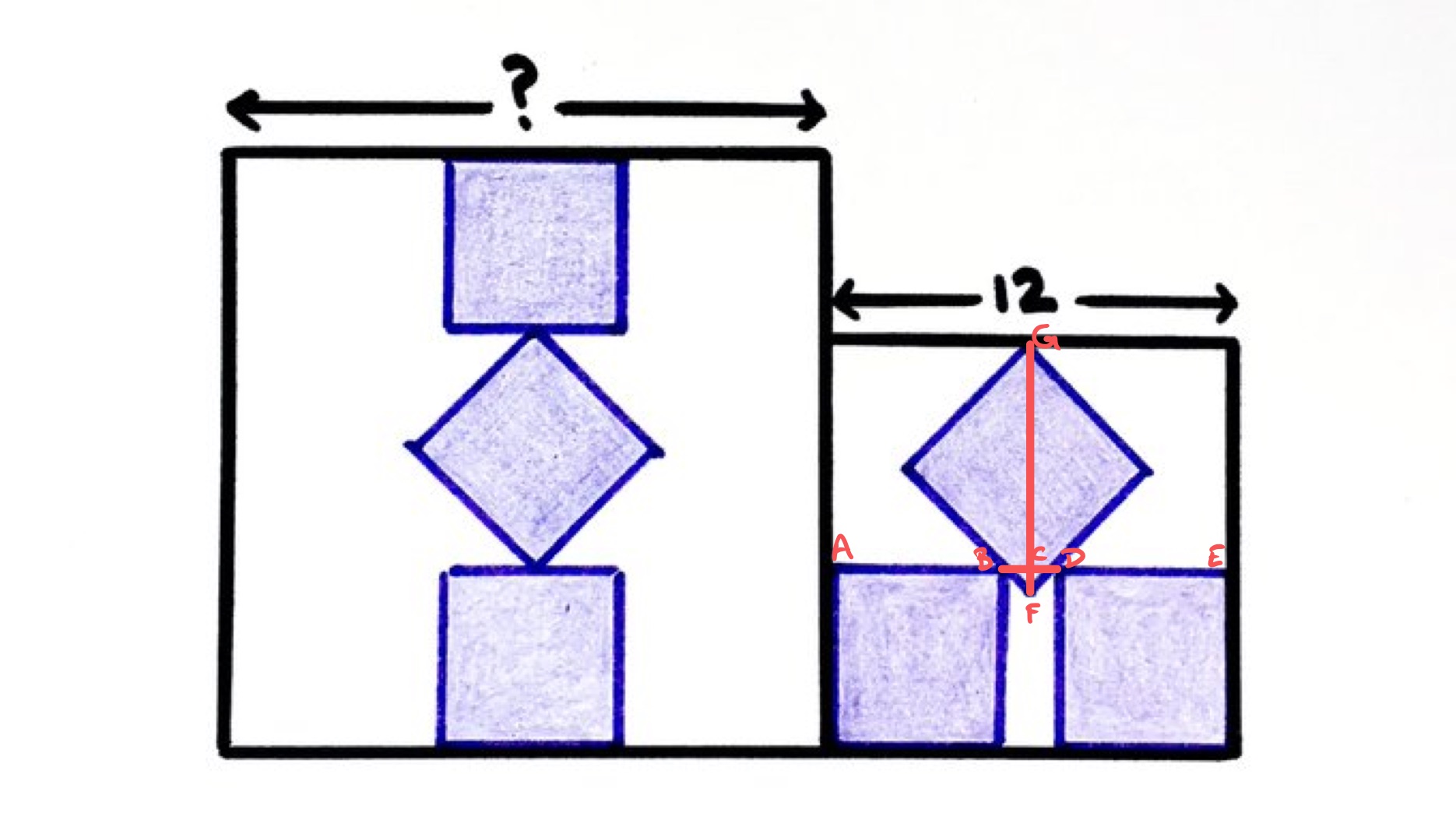
Stacked squares inside two squares labelled

Let $x$ be the side length of one of the purple squares. So $A B$ and $D E$ both have length $x$ . The diagonal of the square is then $\sqrt{2} x$ , so that is the length of $G F$ . Let $y$ be the length of $B C$ , then this is also the length of $C F$ . Then the width of the square is $2 x + 2 y$ and the height is $x + \sqrt{2} x - y$ . As it is a square, these are both equal to $12$ . The length requested is $2 x + \sqrt{2} x$ which can be seen to be equal to:

2 x + \sqrt{2} x = x + \sqrt{2} x - y + x + y = 12 + 6 = 18.

Created on August 17, 2021 21:15:48 by Andrew Stacey

Notes stacked squares inside two squares solution

Solution to the Stacked Squares Inside Two Squares Puzzle

Solution by Lengths in Squares

Notes
stacked squares inside two squares solution