Notes
stacked boxes in circles in squares solution
Solution to the Stacked Boxes in Circles in Squares Puzzle
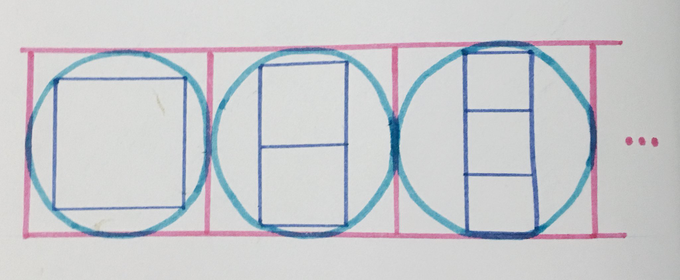
If the area of each pink square is , what’s the area of the blue squares in each box as the sequence continues? Is the total area of the blue squares finite?
Solution by Pythagoras' Theorem
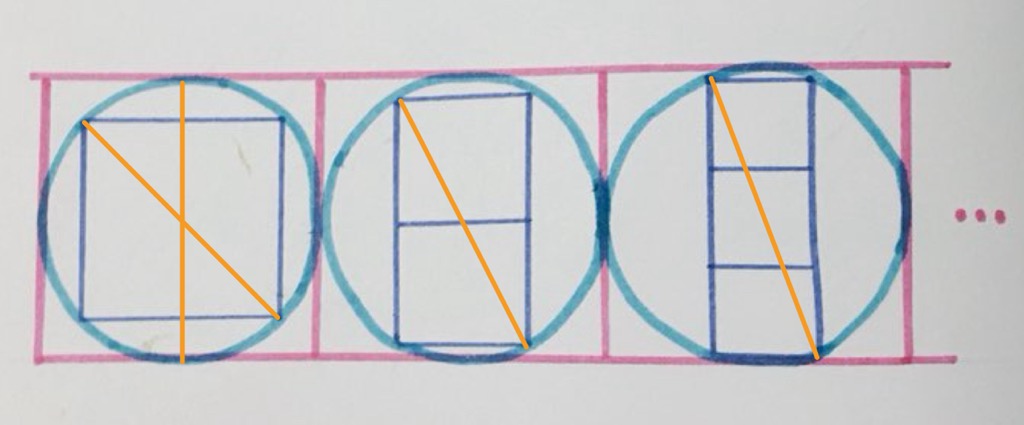
As each pink square has area , it has side length , and so the diameter of each circle is and therefore the diagonal of each rectangle is .
Consider the general case, and let be the number of little squares. Let be the side length of one of the little squares. Then Pythagoras' Theorem states that:
Therefore the total area of the little squares is .
The sum of the areas is therefore:
Since , so . So this series is the harmonic series (except the first term) and so diverges.