Notes
stack of congruent rectangles solution
Solution to the Stack of Congruent Rectangles Puzzle
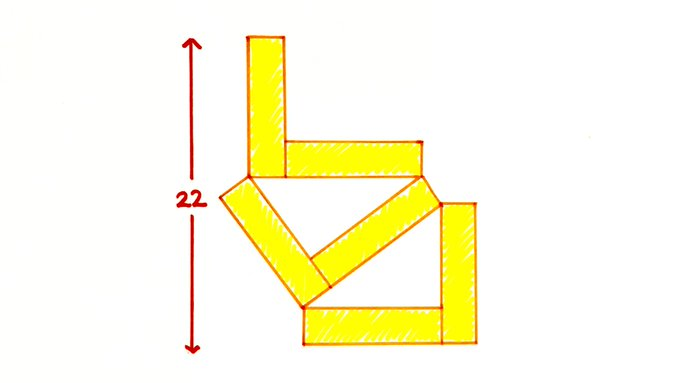
The height of this stack of congruent rectangles is . What’s the total shaded area?
Solution by Similar Triangles and Pythagoras' Theorem
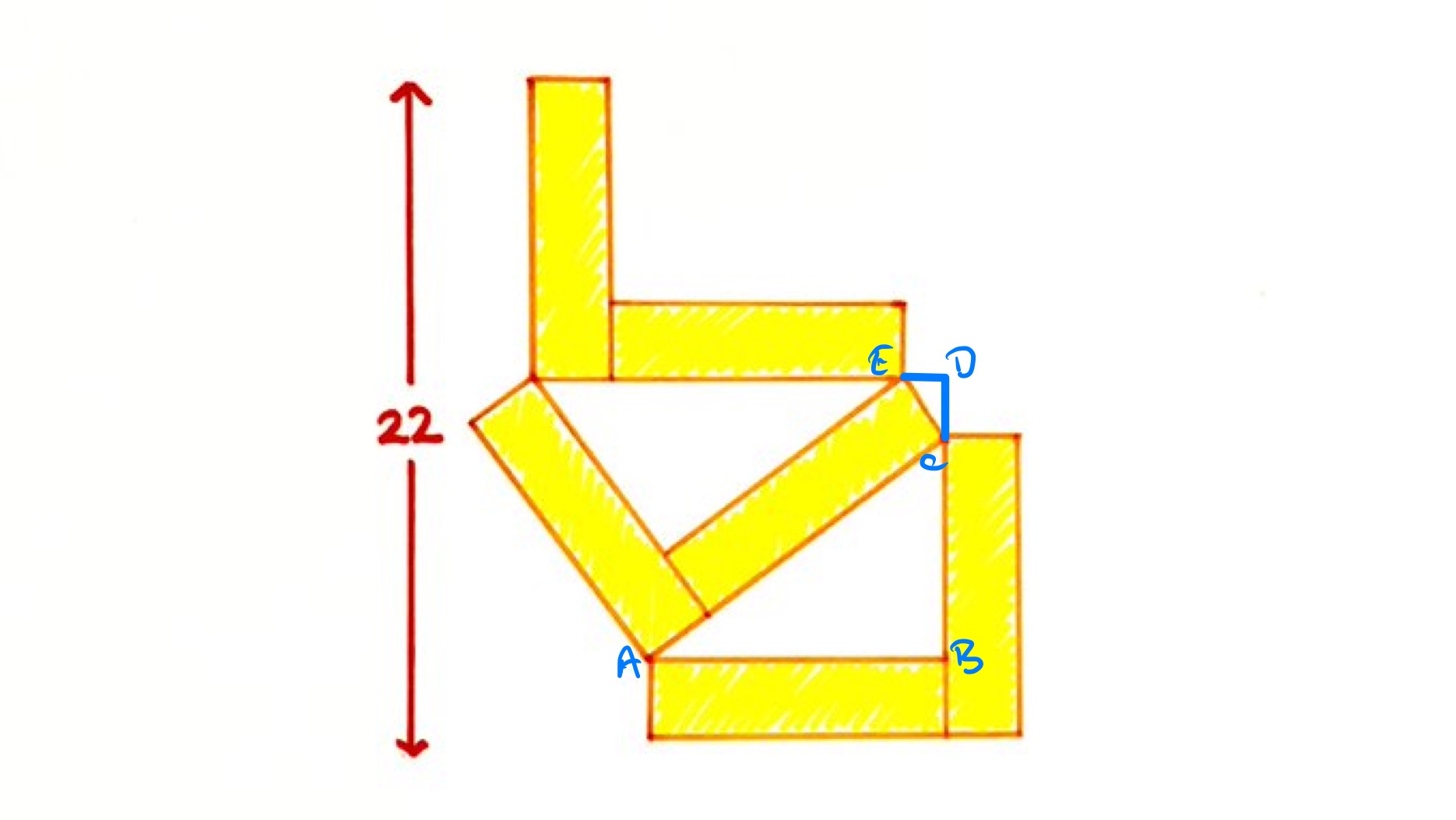
In the diagram above, is the point so that is parallel to and is the continuation of .
Let and be the side lengths of the rectangles, so that has length and has length . Then has length and has length . Triangles and are similar since they are both right-angled triangles and angles and add up to . By comparing with , the scale factor is so the length of is . This means that the total height of the figure is .
Applying Pythagoras' theorem to triangle shows that:
which simplifies to so . Substituting in to the expression for the height, and setting that equal to , gives:
So and . The total area of the rectangles is therefore: