Notes
squares meeting in a circle solution
Squares Meeting in a Circle
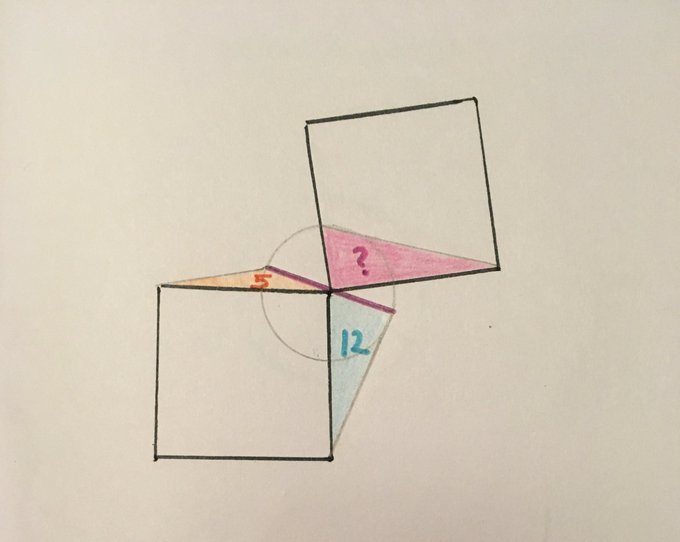
The two squares are identical, and the pink line is a diameter of the circle. What’s the area of the pink triangle?
Solution by Pythagoras' Theorem and Area of a Triangle
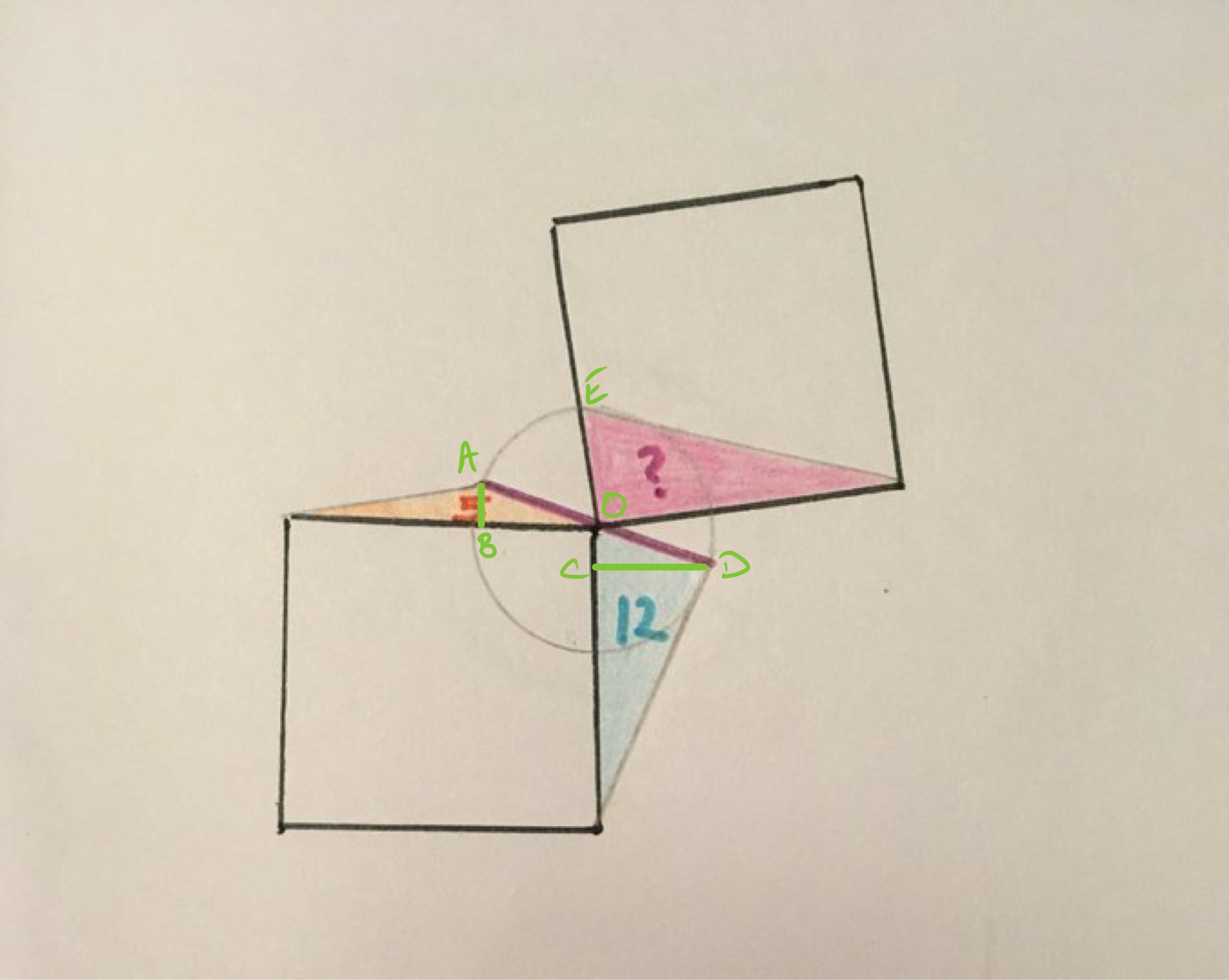
Let be the length of the sides of the squares. As is the height of a triangle with base and area , it has length . Similarly, has length . Triangles and are congruent and are right-angled. Let be the radius of the circle, then by Pythagoras' theorem, . So . The pink triangle therefore has area .