Notes
squares in an octagon solution
Solution to the Squares in an Octagon Problem
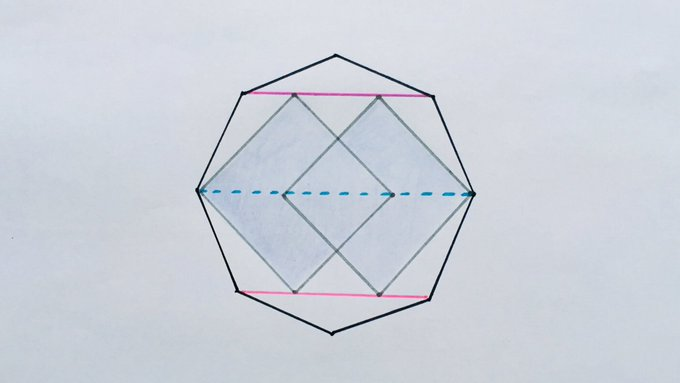
Direct Calculation using Pythagoras’ Theorem
This method uses the fact that the diameter of a square is related to its side length by a factor of .
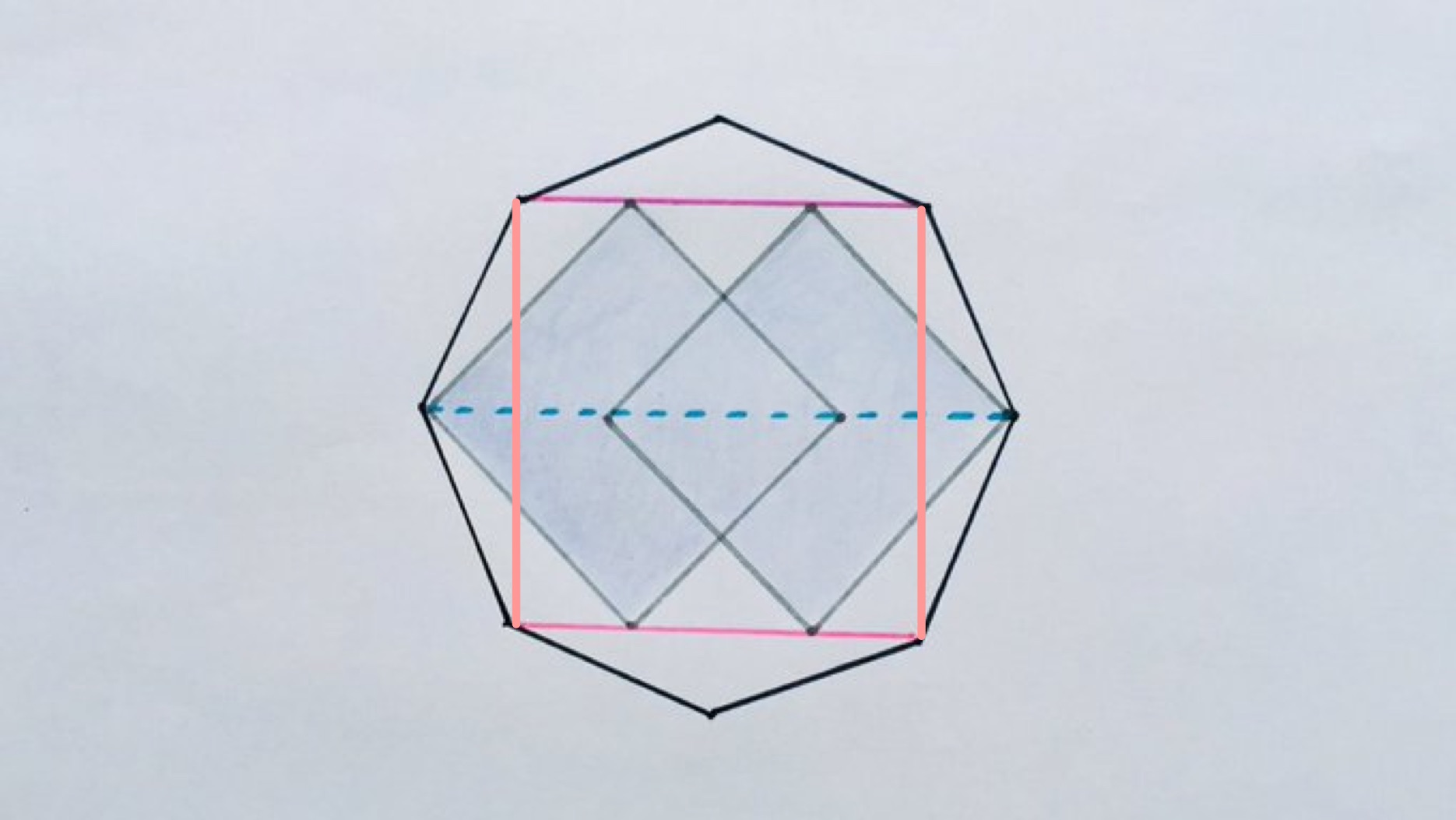
By adding vertical lines at the ends of the pink lines we obtain a larger square inside the octagon. The diameter of this square is the diameter of the octagon, and so using the Pythagorean identity we get that this is . So the dashed blue line has length .
Now consider the medium sized squares. The diameter of these squares is the same as the pink line, so their side length is . Their total perimeter is therefore .
The smallest square, formed by the overlap of the two medium sized squares, has diameter given by taking twice the diameter of the medium sized squares and subtracting the diameter of the octagon, which is . Its perimeter is therefore:
This needs to be taken away from the perimeter of the two medium sized squares to get the perimeter of the shaded octagon:
Symmetry
Adding the vertical lines as in the above method adds some symmetry to the diagram, at least if we ignore the inner squares for the moment. This is only the symmetry of the square, however. To get the full symmetry of the octagon we need to also add lines between the other vertices which results in two overlapping congruent squares.
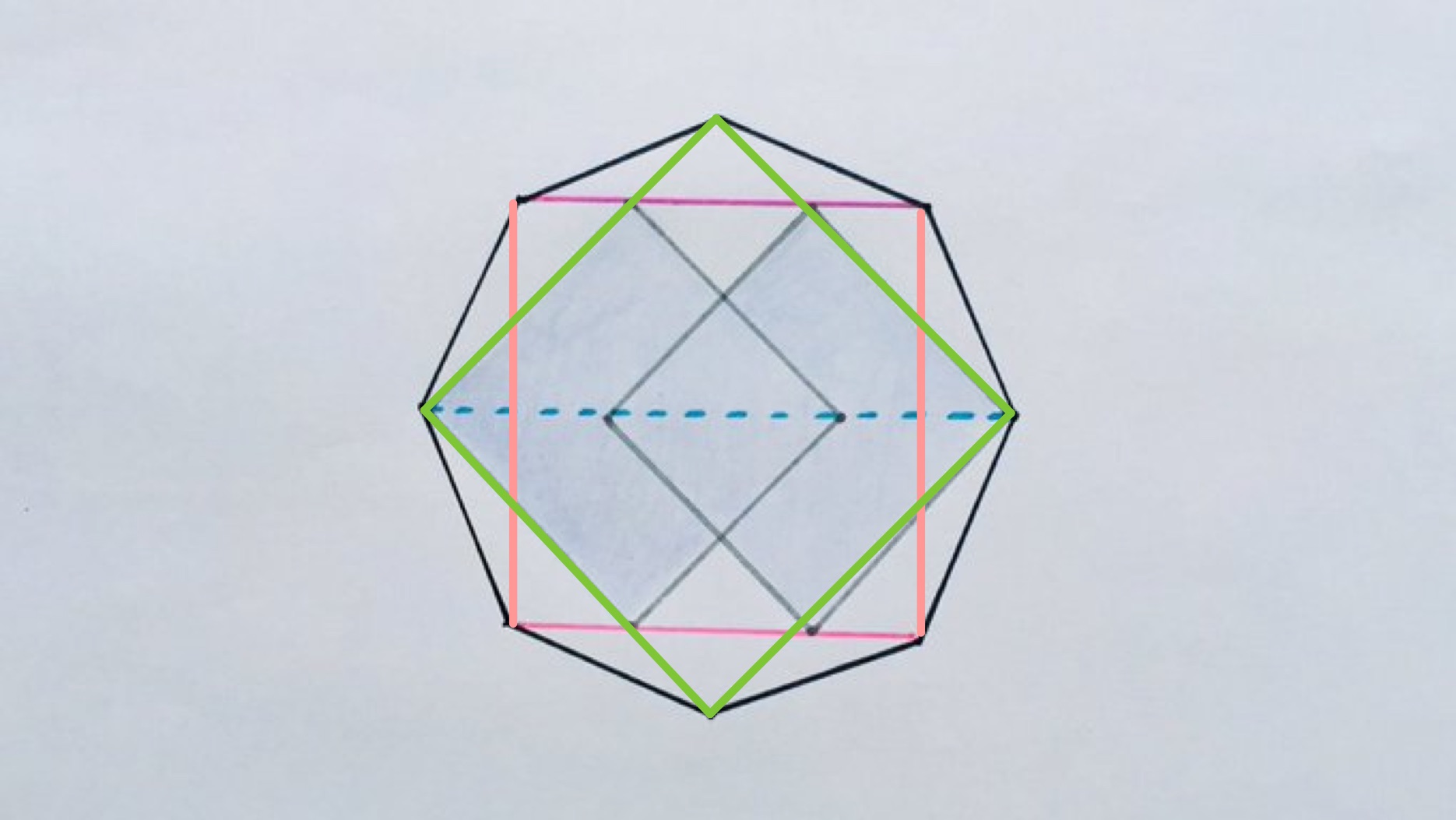
The key to solving this problem is then to observe that the new pink square has the same perimeter as the shaded octagon. Both shapes start at the same vertex with the same interior angle and have a line of symmetry passing through that vertex, so the initial lines must coincide. Where the two shapes diverge, they form a square and each comprises two sides of that square, so the lengths of the sides of the divergent part are the same, and then the last part is coincident again.
Hence the perimeter of the shaded octagon is the same as the square, which is .