Notes
square, rectangle, and two semi-circles solution
Solution to the Square, Rectangle, and Two Semi-Circles Puzzle
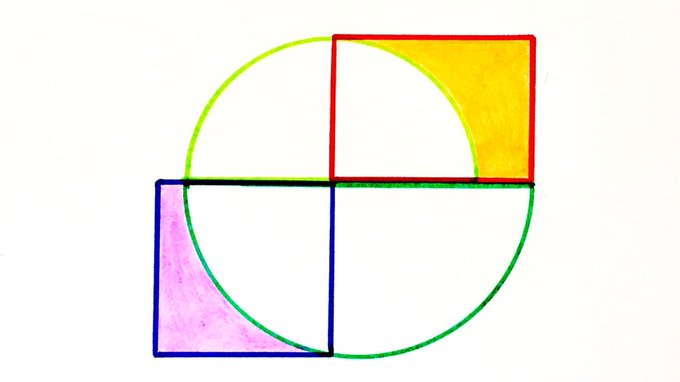
A square, a rectangle and two semicircles. Which shaded area is the larger?
Solution by Pythagoras' Theorem
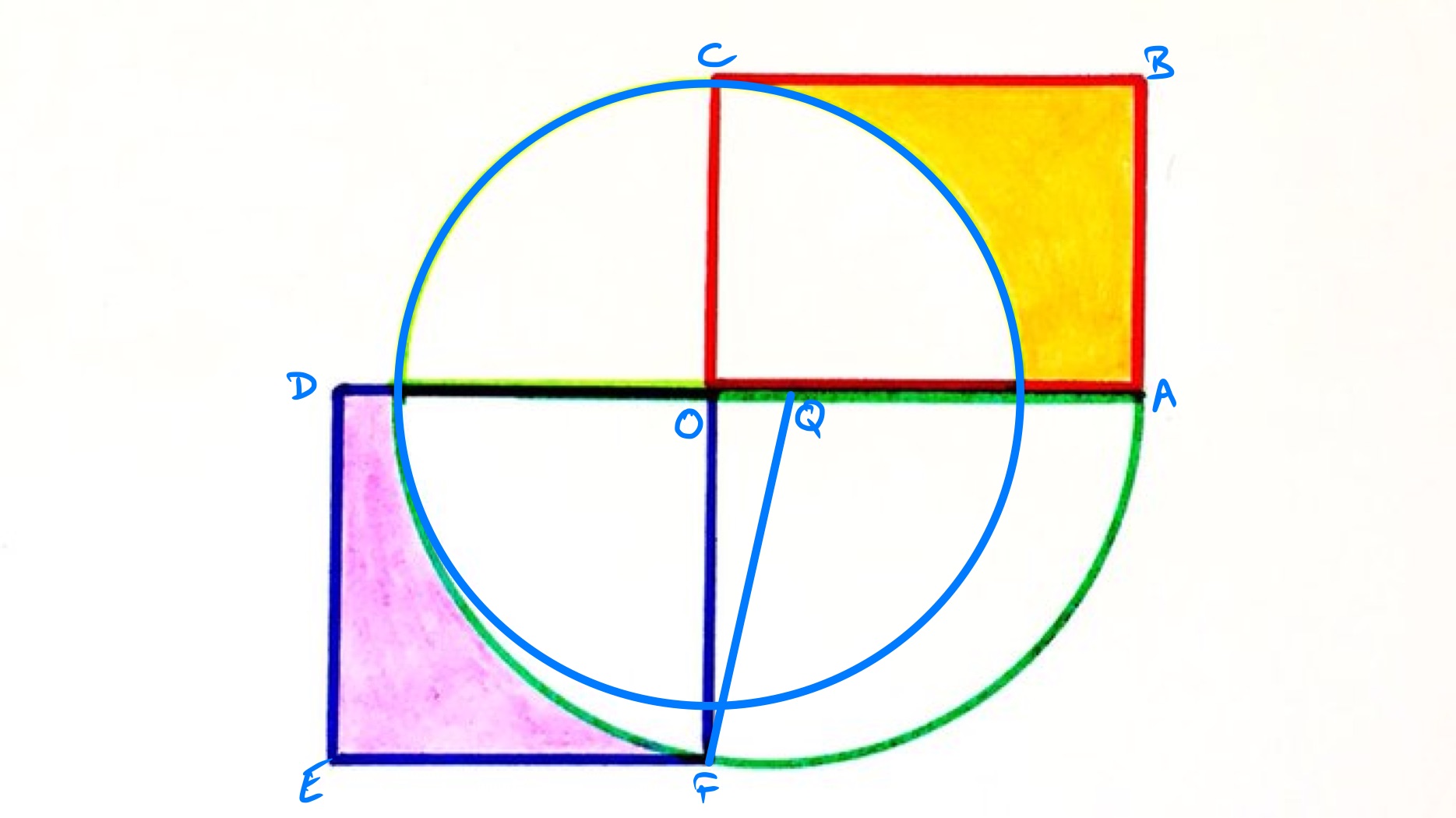
In the above diagram, the points labelled and are the centres of the upper and lower semi-circles respectively. Let be the radius of the upper semi-circle and of the lower. Then has length and has length so the area of rectangle is .
Let be the length of , which is the side length of the purple square. The length of is , so applying Pythagoras' theorem to triangle shows that:
which rearranges to . The square and rectangle therefore have the same area. However, the quarter circle cut out from the rectangle has smaller area than the sector cut out from the square, as can be seen in the diagram by completing the smaller circle to a full circle. Therefore the purple area is smaller than the yellow.