Notes
square overlapping a quarter circle solution
Solution to the Square Overlapping a Quarter Circle Puzzle
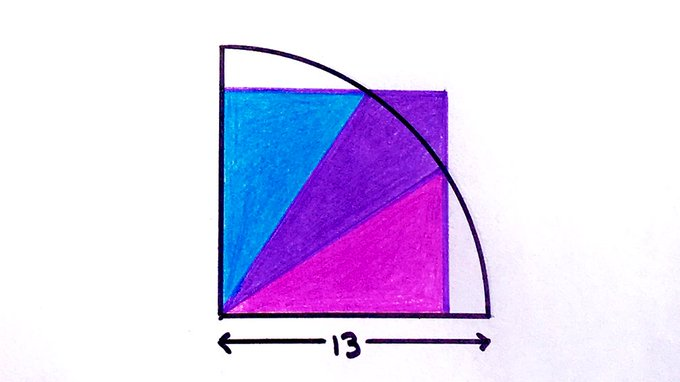
The three coloured sections here have the same area. What’s the total area of the square?
Solution by Area of a Triangle and Pythagoras' Theorem
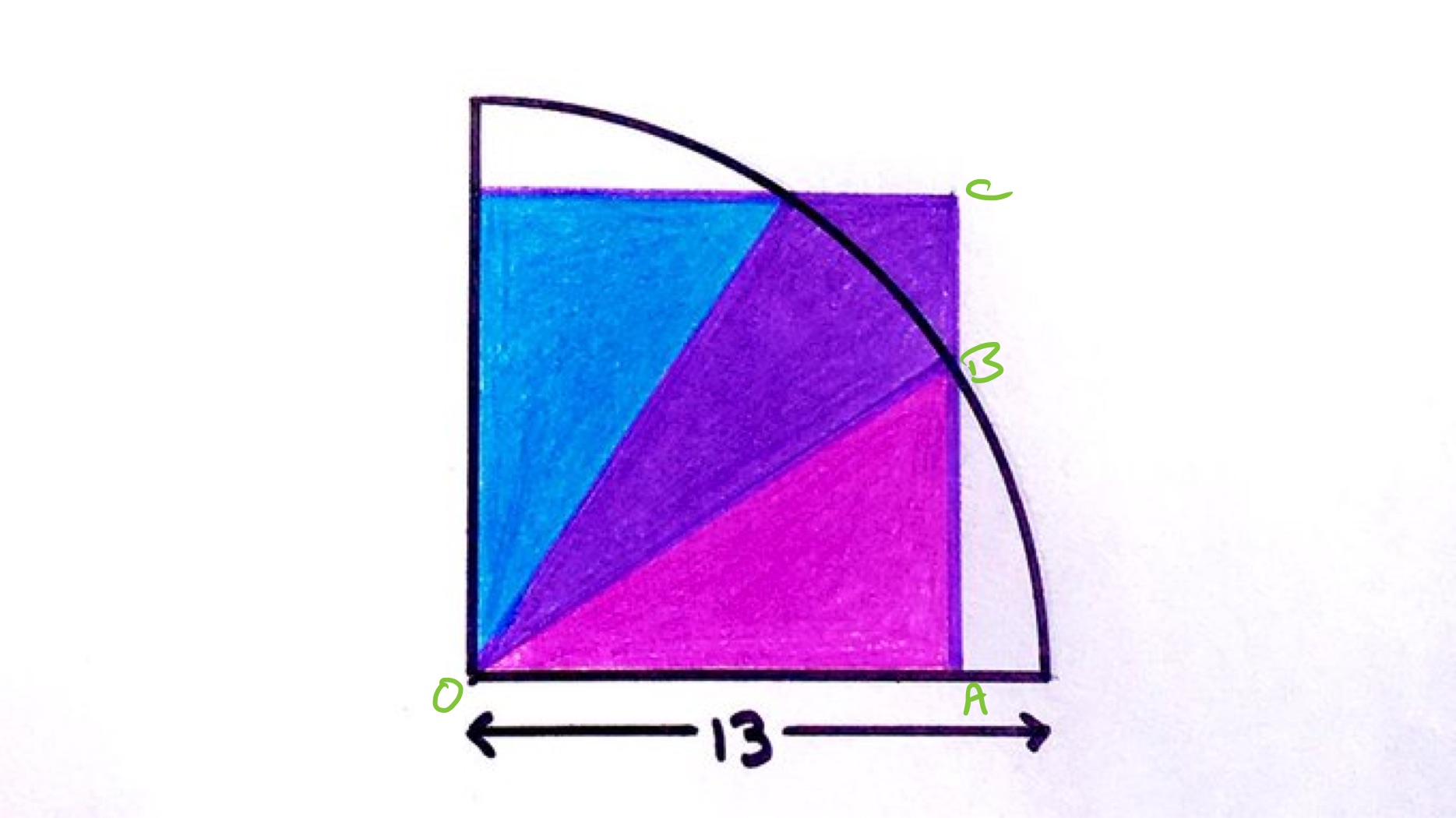
With the points labelled as above, let be the length of so the area of the square is . As the coloured sections have the same area, the area of triangle is a third of that of the square, so from the area of a triangle, has length . Since is a radius of the circle, it has length and so applying Pythagoras' theorem to gives:
This shows that the area of the square is .