Notes
square overlapping a circle solution
Solution to the Square Overlapping a Circle Puzzle
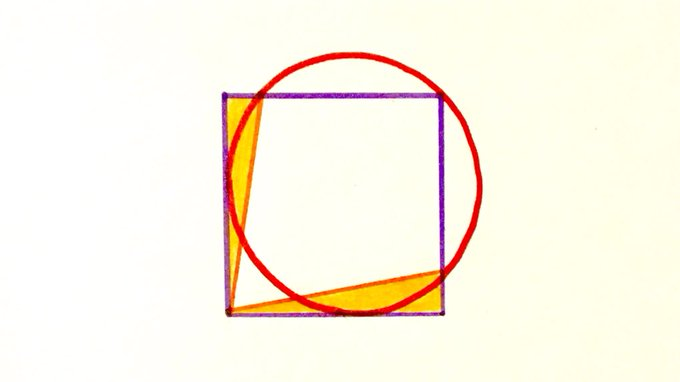
A square, and a circle of radius . What’s the total shaded area?
Solution by Intersecting Chords Theorem
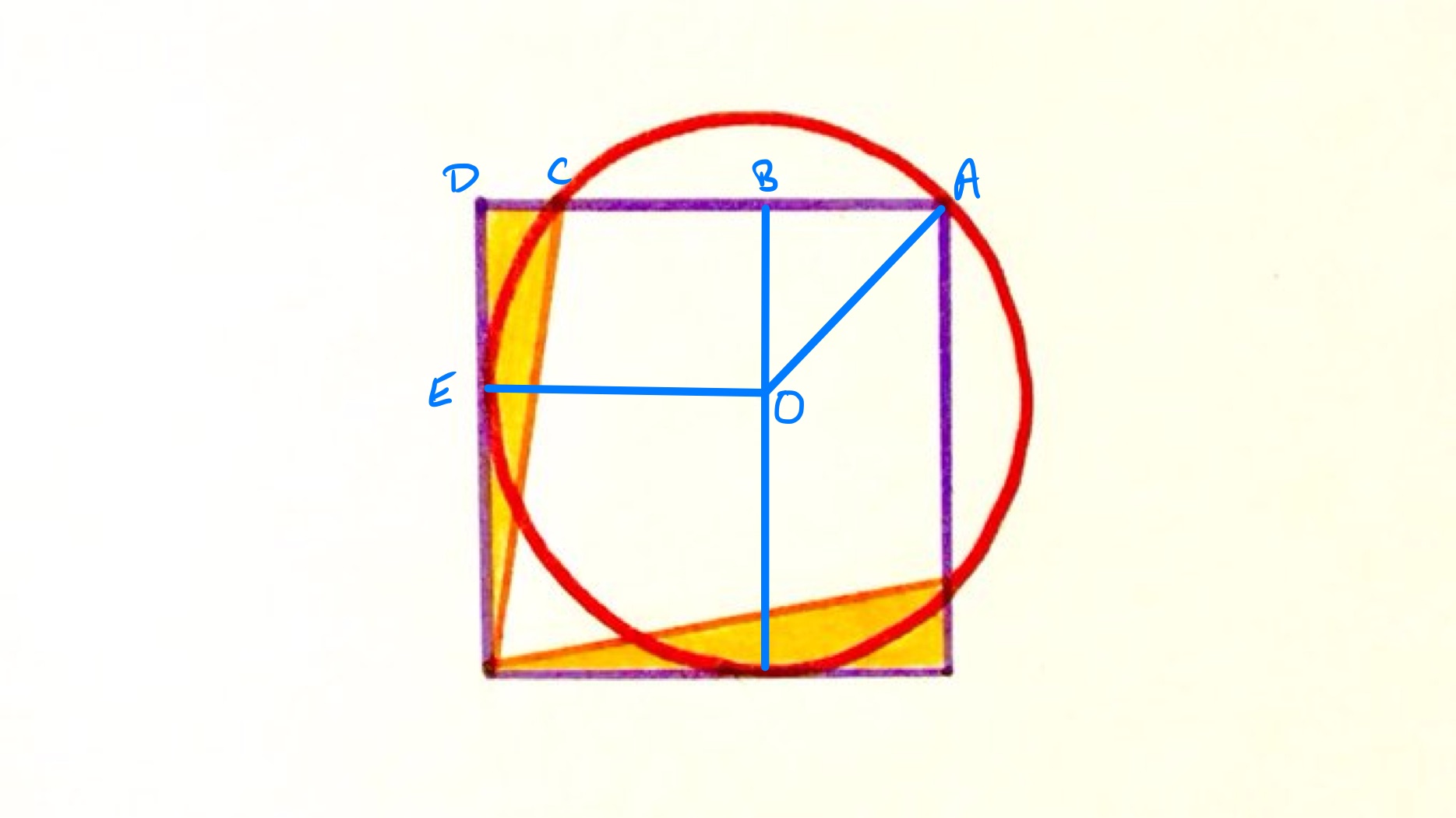
In the diagram above, the point labelled is the centre of the circle. The area of the shaded region is given by multiplying the length of one of the sides of the square by the length of .
The intersecting chords theorem states that , so the shaded region has area equal to the square of the length of . By symmetry, line segment lies on a diagonal of the square, so triangle is isosceles and right-angled. Therefore the square of the length of is half the square of the length of , which is . Since and are congruent, the shaded region thus has area .